Deep Learning: Clustering
Here is my Deep Learning Full Tutorial!
Unsupervised Learning
Clustering
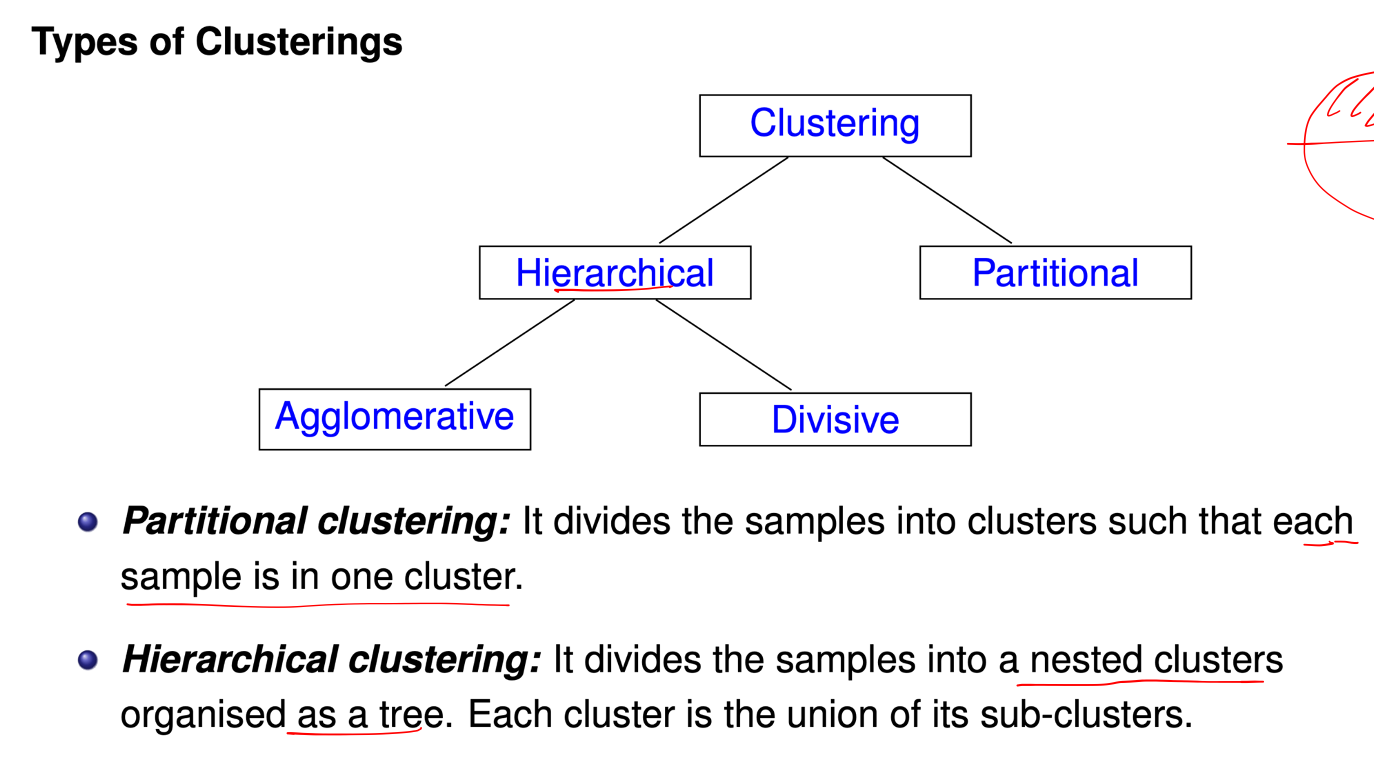
K-means




Kmeans python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np
m = [
[2,2],
[5,1]
]
X = [
[3,4],
[5,1],
[3,7],
[9,6],
[2,2],
[7,0]
]
result = []
while True:
x_m = [(np.array(X) - np.array(center)) for center in m]
distance = [np.sqrt(np.sum(np.power(item,2),axis=1)) for item in x_m]
class_selection = np.argmax(np.transpose(distance),axis=1)
class_num = np.unique(class_selection)
m_prev = m.copy()
for i in range(len(class_num)):
index = np.where(class_selection==class_num[i])[0]
m[i] = np.mean(np.array(X)[index],axis=0)
result = list(np.transpose(np.append(distance,[class_selection],axis=0)).round(4))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('sqrt((x-m1)^2)','sqrt((x-m2)^2)','class'))
for row in result: pt.add_row(row)
print(pt)
print('New Center:',m)
if np.array_equal(np.sort(m_prev),np.sort(m)):
print('Meet Converage!')
break
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
+----------------+----------------+-------+
| sqrt((x-m1)^2) | sqrt((x-m2)^2) | class |
+----------------+----------------+-------+
| 2.2361 | 3.6056 | 1.0 |
| 3.1623 | 0.0 | 0.0 |
| 5.099 | 6.3246 | 1.0 |
| 8.0623 | 6.4031 | 0.0 |
| 0.0 | 3.1623 | 1.0 |
| 5.3852 | 2.2361 | 0.0 |
+----------------+----------------+-------+
New Center: [array([7. , 2.33333333]), array([2.66666667, 4.33333333])]
+----------------+----------------+-------+
| sqrt((x-m1)^2) | sqrt((x-m2)^2) | class |
+----------------+----------------+-------+
| 4.3333 | 0.4714 | 0.0 |
| 2.4037 | 4.0689 | 1.0 |
| 6.1464 | 2.6874 | 0.0 |
| 4.1767 | 6.549 | 1.0 |
| 5.0111 | 2.4267 | 0.0 |
| 2.3333 | 6.1283 | 1.0 |
+----------------+----------------+-------+
New Center: [array([2.66666667, 4.33333333]), array([7. , 2.33333333])]
Fuzzy K-means



Fuzzy K means python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
X = [
[-1,3],
[1,4],
[0,5],
[4,-1],
[3,0],
[5,1]
]
# disable Scientific notation
np.set_printoptions(suppress=True)
# cluster number
K = 2
# parameter b
b = 2
# theta, terminate state, change smaller than t
t = 0.5
# initial membership
u = [
[1,0],
[0.5,0.5],
[0.5,0.5],
[0.5,0.5],
[0.5,0.5],
[0,1]
]
# normalise membership
u = [(item/np.sum(item)) for item in u]
counter = 0
while True:
if counter > 0:
m_prev = m
u_transpose = np.transpose(u)
m = np.dot(np.power(u_transpose,2),X)/np.sum(np.power(u_transpose,2),axis=1)
result = []
for index in range(len(X)):
x = X[index]
x_m = [(np.array(x) - np.array(center)) for center in m]
distance = [np.sqrt(np.sum(np.power(item,2))) for item in x_m]
distance_inverse = np.power([1/item for item in distance],2)
u_update = distance_inverse/sum(distance_inverse)
u[index] = u_update
result.append((index+1,X[index],np.round(m,4),np.round(distance,4),np.round(distance_inverse,4),np.round(u[index],4)))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration','Sample X','cluster center m','sqrt(X-m)^2','(1/sqrt(X-m)^2)^2','ui'))
for row in result: pt.add_row(row)
print(pt)
for index in range(len(m)):
print('m'+str(index+1),':',np.round(m[index],4))
if counter > 0:
compare = m_prev - m
if np.all(np.abs(compare)< t):
print('Meet Converage!')
break
counter += 1
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
+-----------+----------+------------------+-----------------+-------------------+-----------------+
| iteration | Sample X | cluster center m | sqrt(X-m)^2 | (1/sqrt(X-m)^2)^2 | ui |
+-----------+----------+------------------+-----------------+-------------------+-----------------+
| 1 | [-1, 3] | [[0.5 2.5] | [1.5811 4.7434] | [0.4 0.0444] | [0.9 0.1] |
| | | [3.5 1.5]] | | | |
| 2 | [1, 4] | [[0.5 2.5] | [1.5811 3.5355] | [0.4 0.08] | [0.8333 0.1667] |
| | | [3.5 1.5]] | | | |
| 3 | [0, 5] | [[0.5 2.5] | [2.5495 4.9497] | [0.1538 0.0408] | [0.7903 0.2097] |
| | | [3.5 1.5]] | | | |
| 4 | [4, -1] | [[0.5 2.5] | [4.9497 2.5495] | [0.0408 0.1538] | [0.2097 0.7903] |
| | | [3.5 1.5]] | | | |
| 5 | [3, 0] | [[0.5 2.5] | [3.5355 1.5811] | [0.08 0.4 ] | [0.1667 0.8333] |
| | | [3.5 1.5]] | | | |
| 6 | [5, 1] | [[0.5 2.5] | [4.7434 1.5811] | [0.0444 0.4 ] | [0.1 0.9] |
| | | [3.5 1.5]] | | | |
+-----------+----------+------------------+-----------------+-------------------+-----------------+
m1 : [0.5 2.5]
m2 : [3.5 1.5]
+-----------+----------+-------------------+-----------------+-------------------+-----------------+
| iteration | Sample X | cluster center m | sqrt(X-m)^2 | (1/sqrt(X-m)^2)^2 | ui |
+-----------+----------+-------------------+-----------------+-------------------+-----------------+
| 1 | [-1, 3] | [[0.0876 3.7529] | [1.3228 5.6312] | [0.5715 0.0315] | [0.9477 0.0523] |
| | | [3.9124 0.2471]] | | | |
| 2 | [1, 4] | [[0.0876 3.7529] | [0.9453 4.7504] | [1.1191 0.0443] | [0.9619 0.0381] |
| | | [3.9124 0.2471]] | | | |
| 3 | [0, 5] | [[0.0876 3.7529] | [1.2502 6.156 ] | [0.6398 0.0264] | [0.9604 0.0396] |
| | | [3.9124 0.2471]] | | | |
| 4 | [4, -1] | [[0.0876 3.7529] | [6.156 1.2502] | [0.0264 0.6398] | [0.0396 0.9604] |
| | | [3.9124 0.2471]] | | | |
| 5 | [3, 0] | [[0.0876 3.7529] | [4.7504 0.9453] | [0.0443 1.1191] | [0.0381 0.9619] |
| | | [3.9124 0.2471]] | | | |
| 6 | [5, 1] | [[0.0876 3.7529] | [5.6312 1.3228] | [0.0315 0.5715] | [0.0523 0.9477] |
| | | [3.9124 0.2471]] | | | |
+-----------+----------+-------------------+-----------------+-------------------+-----------------+
m1 : [0.0876 3.7529]
m2 : [3.9124 0.2471]
+-----------+----------+---------------------+-----------------+-------------------+-----------------+
| iteration | Sample X | cluster center m | sqrt(X-m)^2 | (1/sqrt(X-m)^2)^2 | ui |
+-----------+----------+---------------------+-----------------+-------------------+-----------------+
| 1 | [-1, 3] | [[ 0.0187 4.0009] | [1.4281 5.8154] | [0.4903 0.0296] | [0.9431 0.0569] |
| | | [ 3.9813 -0.0009]] | | | |
| 2 | [1, 4] | [[ 0.0187 4.0009] | [0.9813 4.9895] | [1.0385 0.0402] | [0.9628 0.0372] |
| | | [ 3.9813 -0.0009]] | | | |
| 3 | [0, 5] | [[ 0.0187 4.0009] | [0.9993 6.3921] | [1.0014 0.0245] | [0.9761 0.0239] |
| | | [ 3.9813 -0.0009]] | | | |
| 4 | [4, -1] | [[ 0.0187 4.0009] | [6.3921 0.9993] | [0.0245 1.0014] | [0.0239 0.9761] |
| | | [ 3.9813 -0.0009]] | | | |
| 5 | [3, 0] | [[ 0.0187 4.0009] | [4.9895 0.9813] | [0.0402 1.0385] | [0.0372 0.9628] |
| | | [ 3.9813 -0.0009]] | | | |
| 6 | [5, 1] | [[ 0.0187 4.0009] | [5.8154 1.4281] | [0.0296 0.4903] | [0.0569 0.9431] |
| | | [ 3.9813 -0.0009]] | | | |
+-----------+----------+---------------------+-----------------+-------------------+-----------------+
m1 : [0.0187 4.0009]
m2 : [ 3.9813 -0.0009]
Meet Converage!
Iterative Optimization




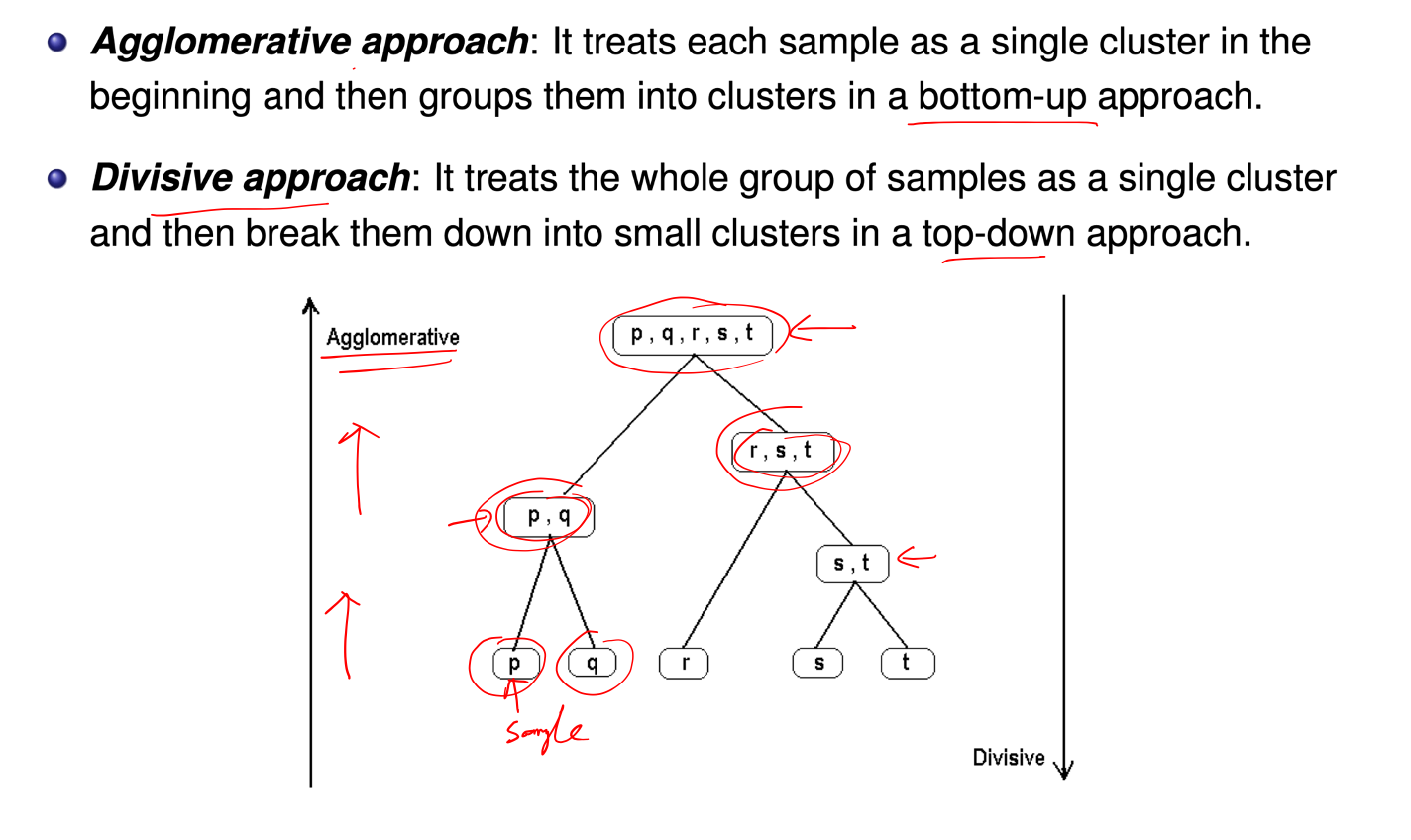
Hierarchical Clustering



hierarchical agglomerative python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
import numpy as np
from prettytable import PrettyTable
X = [
[-1,3],
[1,2],
[0,1],
[4,0],
[5,4],
[3,2]
]
# terminate state, cluster = 3
c = 3
def get_mean(input,y=0):
if len(np.shape(input))>1:
return np.mean(input,axis=0)
else:
return input
def get_mean_distance(x,y):
m = get_mean(x)
n = get_mean(y)
return np.sqrt(np.sum(np.power(np.array(m)-np.array(n),2)))
def get_avg_distance(x,y):
distance = []
if len(np.shape(x))>1 and len(np.shape(y))>1:
for m in x:
for n in y:
distance.append(np.sqrt(np.sum(np.power(np.array(m)-np.array(n),2))))
return np.mean(distance)
elif len(np.shape(x))>1 and len(np.shape(y))<=1:
for m in x:
distance.append(np.sqrt(np.sum(np.power(np.array(m)-np.array(y),2))))
return np.mean(distance)
elif len(np.shape(x))<=1 and len(np.shape(y))>1:
for m in y:
distance.append(np.sqrt(np.sum(np.power(np.array(m)-np.array(x),2))))
return np.mean(distance)
else:
return np.sqrt(np.sum(np.power(np.array(x)-np.array(y),2)))
def get_max_distance(x,y):
best = 0
if len(np.shape(x))>1 and len(np.shape(y))>1:
for m in x:
for n in y:
distance = np.sqrt(np.sum(np.power(np.array(m)-np.array(n),2)))
if distance > best:
best = distance
return best
elif len(np.shape(x))>1 and len(np.shape(y))<=1:
for m in x:
distance = np.sqrt(np.sum(np.power(np.array(m)-np.array(y),2)))
if distance > best:
best = distance
return best
elif len(np.shape(x))<=1 and len(np.shape(y))>1:
for m in y:
distance = np.sqrt(np.sum(np.power(np.array(m)-np.array(x),2)))
if distance > best:
best = distance
return best
else:
return np.sqrt(np.sum(np.power(np.array(x)-np.array(y),2)))
def get_min_distance(x,y):
best = 9999
if len(np.shape(x))>1 and len(np.shape(y))>1:
for m in x:
for n in y:
distance = np.sqrt(np.sum(np.power(np.array(m)-np.array(n),2)))
if distance < best:
best = distance
return best
elif len(np.shape(x))>1 and len(np.shape(y))<=1:
for m in x:
distance = np.sqrt(np.sum(np.power(np.array(m)-np.array(y),2)))
if distance < best:
best = distance
return best
elif len(np.shape(x))<=1 and len(np.shape(y))>1:
for m in y:
distance = np.sqrt(np.sum(np.power(np.array(m)-np.array(x),2)))
if distance < best:
best = distance
return best
else:
return np.sqrt(np.sum(np.power(np.array(x)-np.array(y),2)))
def add_list(x,y):
if len(np.shape(x))>1 and len(np.shape(y))>1:
return x+y
elif len(np.shape(x))<=1 and len(np.shape(y))>1:
return y+[x]
elif len(np.shape(x))>1 and len(np.shape(y))<=1:
return x+[y]
else:
return [x,y]
X_new = X
for index in range(len(X_new)):
print('Cluster',index+1,':',X_new[index])
while True:
best = 10000
result = []
for x_index in range(len(X_new)-1):
x = X_new[x_index]
y = X_new[x_index+1:]
distance = [get_min_distance(x,m) for m in y]
result.append([x_index+1] + list(np.append(np.ones(x_index+1)*0,np.round(distance,4))))
if best>np.min(distance):
best_list = add_list(X_new[x_index],X_new[x_index + np.argmin(distance) + 1])
best_index = [x_index,x_index + np.argmin(distance) + 1]
best = np.min(distance)
# prettytable
# -----------------------------------------------------------
title = ['xi']+[str(i) for i in list(range(1,len(X_new)+1))]
pt = PrettyTable(title)
for row in result: pt.add_row(row)
print(pt)
# update X
X_new = np.delete(X_new,best_index,axis=0)
X_new = [best_list] + X_new.tolist()
for index in range(len(X_new)):
print('Cluster',index+1,':',X_new[index])
if len(X_new) <=3 :
break
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
Cluster 1 : [-1, 3]
Cluster 2 : [1, 2]
Cluster 3 : [0, 1]
Cluster 4 : [4, 0]
Cluster 5 : [5, 4]
Cluster 6 : [3, 2]
+----+-----+--------+--------+--------+--------+--------+
| xi | 1 | 2 | 3 | 4 | 5 | 6 |
+----+-----+--------+--------+--------+--------+--------+
| 1 | 0.0 | 2.2361 | 2.2361 | 5.831 | 6.0828 | 4.1231 |
| 2 | 0.0 | 0.0 | 1.4142 | 3.6056 | 4.4721 | 2.0 |
| 3 | 0.0 | 0.0 | 0.0 | 4.1231 | 5.831 | 3.1623 |
| 4 | 0.0 | 0.0 | 0.0 | 0.0 | 4.1231 | 2.2361 |
| 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.8284 |
+----+-----+--------+--------+--------+--------+--------+
Cluster 1 : [[1, 2], [0, 1]]
Cluster 2 : [-1, 3]
Cluster 3 : [4, 0]
Cluster 4 : [5, 4]
Cluster 5 : [3, 2]
+----+-----+--------+--------+--------+--------+
| xi | 1 | 2 | 3 | 4 | 5 |
+----+-----+--------+--------+--------+--------+
| 1 | 0.0 | 2.2361 | 3.8643 | 5.1515 | 2.5811 |
| 2 | 0.0 | 0.0 | 5.831 | 6.0828 | 4.1231 |
| 3 | 0.0 | 0.0 | 0.0 | 4.1231 | 2.2361 |
| 4 | 0.0 | 0.0 | 0.0 | 0.0 | 2.8284 |
+----+-----+--------+--------+--------+--------+
Cluster 1 : [[1, 2], [0, 1], [-1, 3]]
Cluster 2 : [4, 0]
Cluster 3 : [5, 4]
Cluster 4 : [3, 2]
+----+-----+--------+--------+--------+
| xi | 1 | 2 | 3 | 4 |
+----+-----+--------+--------+--------+
| 1 | 0.0 | 4.5199 | 5.462 | 3.0951 |
| 2 | 0.0 | 0.0 | 4.1231 | 2.2361 |
| 3 | 0.0 | 0.0 | 0.0 | 2.8284 |
+----+-----+--------+--------+--------+
Cluster 1 : [[4, 0], [3, 2]]
Cluster 2 : [[1, 2], [0, 1], [-1, 3]]
Cluster 3 : [5, 4]
Competitive Learning




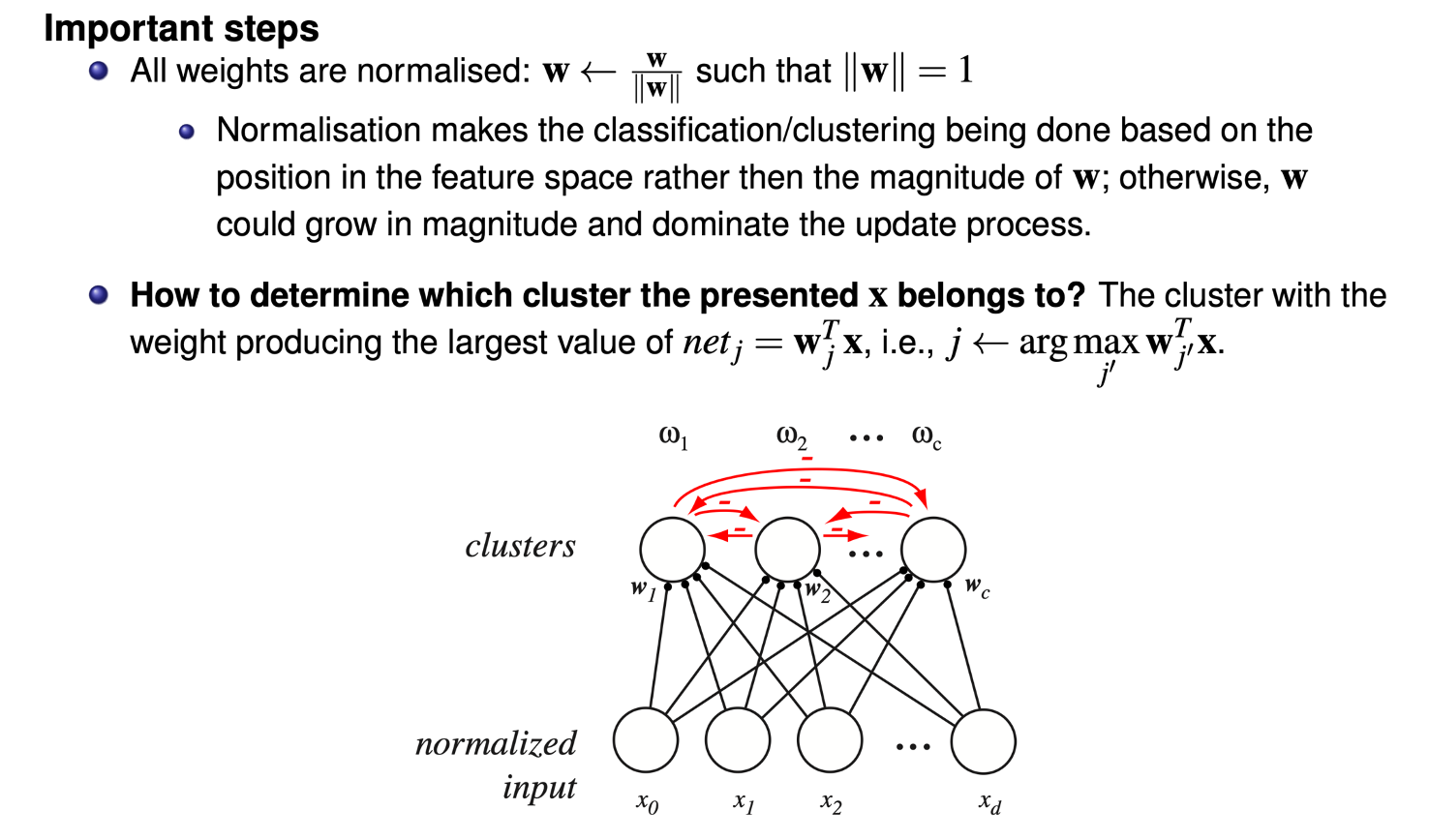


Competitive learning alogrithm without normalization python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
m = [
[-0.5,1.5],
[0,2.5],
[1.5,0]
]
X = [
[-1,3],
[1,4],
[0,5],
[4,-1],
[3,0],
[5,1]
]
# learning rate
n = 0.1
sample = [
[0,5],
[-1,3],
[-1,3],
[3,0],
[5,1]
]
result = []
for index in range(len(sample)):
x = sample[index]
x_m = [(np.array(x) - np.array(center)) for center in m]
distance = [np.sqrt(np.sum(np.power(item,2))) for item in x_m]
j = np.argmin(distance)
m[j] = np.array(m[j]) + n*(x - np.array(m[j]))
result.append((index+1,sample[index],np.round(distance,4),j+1,m[j]))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration','Sample X','sqrt(X-m)^2','j = argmin(x-mj)','mj'))
for row in result: pt.add_row(row)
print(pt)
for index in range(len(m)):
print('m'+str(index+1),':',m[index])
Output
1
2
3
4
5
6
7
8
9
10
11
12
+-----------+----------+------------------------+------------------+-------------------+
| iteration | Sample X | sqrt(X-m)^2 | j = argmin(x-mj) | mj |
+-----------+----------+------------------------+------------------+-------------------+
| 1 | [0, 5] | [3.5355 2.5 5.2202] | 2 | [0. 2.75] |
| 2 | [-1, 3] | [1.5811 1.0308 3.9051] | 2 | [-0.1 2.775] |
| 3 | [-1, 3] | [1.5811 0.9277 3.9051] | 2 | [-0.19 2.7975] |
| 4 | [3, 0] | [3.8079 4.2429 1.5 ] | 3 | [1.65 0. ] |
| 5 | [5, 1] | [5.5227 5.4925 3.4961] | 3 | [1.985 0.1 ] |
+-----------+----------+------------------------+------------------+-------------------+
m1 : [-0.5, 1.5]
m2 : [-0.19 2.7975]
m3 : [1.985 0.1 ]
Clustering for Unknown Number of Clusters




Basic leader follower algorithm python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
X = [
[-1,3],
[1,4],
[0,5],
[4,-1],
[3,0],
[5,1]
]
# theta
o = 3
# learning rate
n = 0.5
sample = [
[0,5],
[-1,3],
[-1,3],
[3,0],
[5,1]
]
m = []
result = []
for index in range(len(sample)):
x = sample[index]
if len(m) == 0:
m.append(x)
m_prev = m.copy()
x_m = [(np.array(x) - np.array(center)) for center in m]
distance = [np.sqrt(np.sum(np.power(item,2))) for item in x_m]
j = np.argmin(distance)
if distance[j] < o:
m[j] = np.array(m[j]) + n*(x - np.array(m[j]))
else:
m.append(x)
result.append((index+1,sample[index],np.array(m_prev).round(4),np.round(distance,4),j+1,(distance[j]<o),np.array(m).round(4)))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration','Sample X','cluster center m','sqrt(X-m)^2','j = argmin(x-mj)','|x-m| < theta','mj = mj+n(x-mj)'))
for row in result: pt.add_row(row)
print(pt)
for index in range(len(m)):
print('m'+str(index+1),':',m[index])
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
+-----------+----------+------------------+-----------------+------------------+---------------+-----------------+
| iteration | Sample X | cluster center m | sqrt(X-m)^2 | j = argmin(x-mj) | |x-m| < theta | mj = mj+n(x-mj) |
+-----------+----------+------------------+-----------------+------------------+---------------+-----------------+
| 1 | [0, 5] | [[0 5]] | [0.] | 1 | True | [[0. 5.]] |
| 2 | [-1, 3] | [[0. 5.]] | [2.2361] | 1 | True | [[-0.5 4. ]] |
| 3 | [-1, 3] | [[-0.5 4. ]] | [1.118] | 1 | True | [[-0.75 3.5 ]] |
| 4 | [3, 0] | [[-0.75 3.5 ]] | [5.1296] | 1 | False | [[-0.75 3.5 ] |
| | | | | | | [ 3. 0. ]] |
| 5 | [5, 1] | [[-0.75 3.5 ] | [6.27 2.2361] | 2 | True | [[-0.75 3.5 ] |
| | | [ 3. 0. ]] | | | | [ 4. 0.5 ]] |
+-----------+----------+------------------+-----------------+------------------+---------------+-----------------+
m1 : [-0.75 3.5 ]
m2 : [4. 0.5]
Comments powered by Disqus.