Home Neural Networks
Post
Cancel

Neural Networks

Posted Feb 11, 2022 Updated Sep 12, 2022
By Weizhi Peng
8 min read

Deep Learning: Neural Networks

Here is my Deep Learning Full Tutorial!

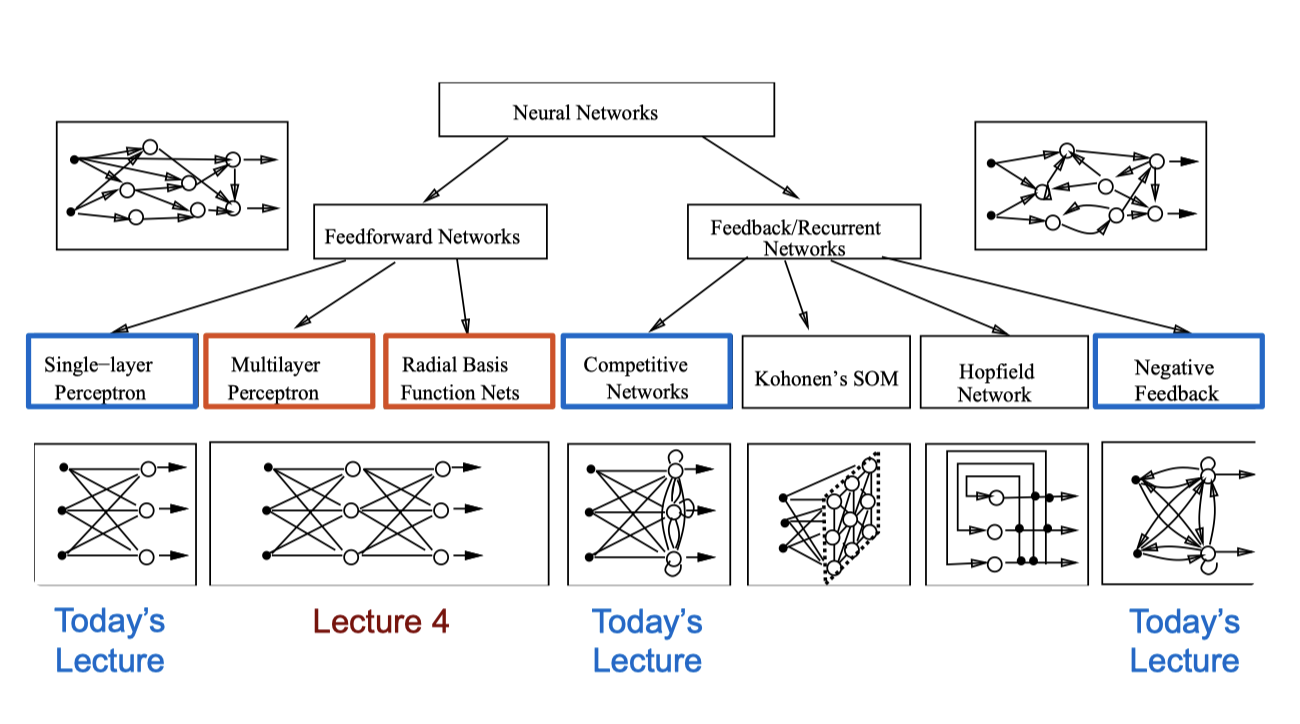
Screen Shot 2022-05-12 at 15.02.35.png

Screen Shot 2022-05-12 at 13.18.53.png

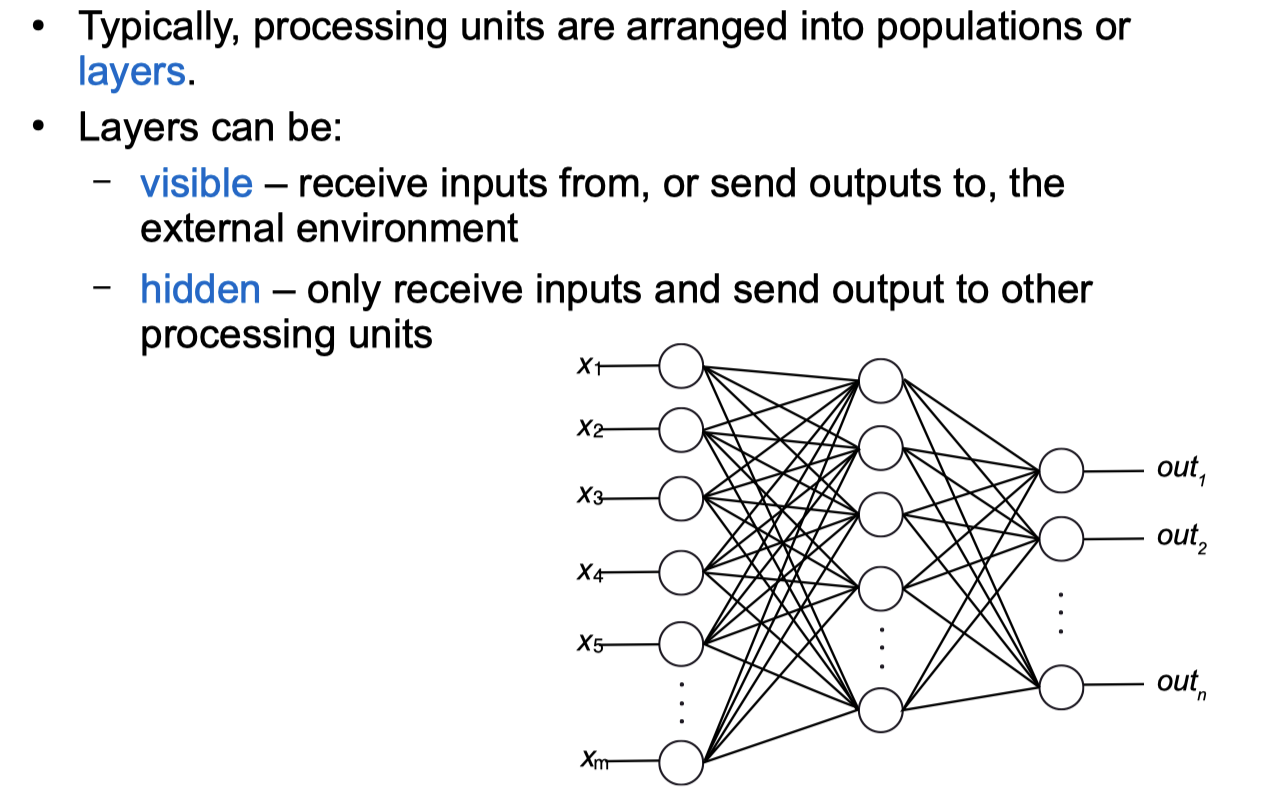
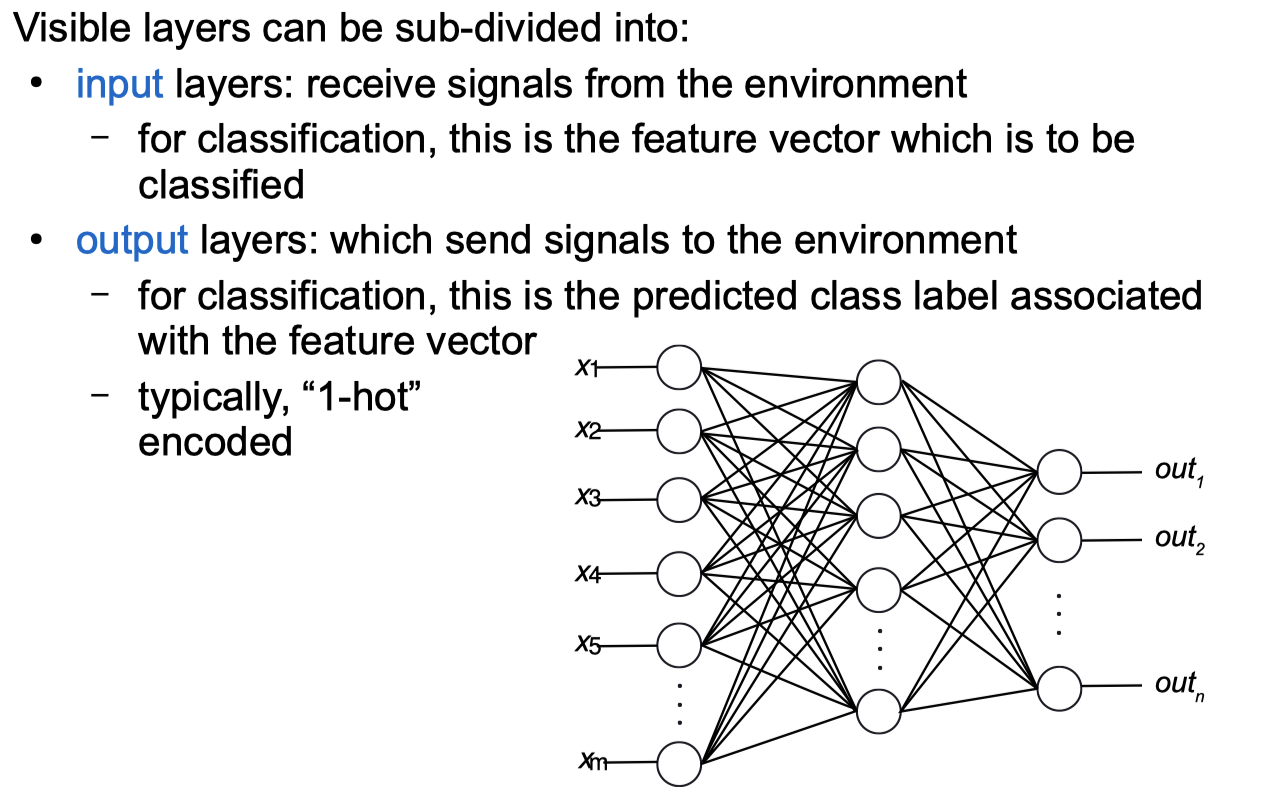
Neural Networks

Screen Shot 2022-05-12 at 13.19.41.png

Screen Shot 2022-05-12 at 13.19.52.png

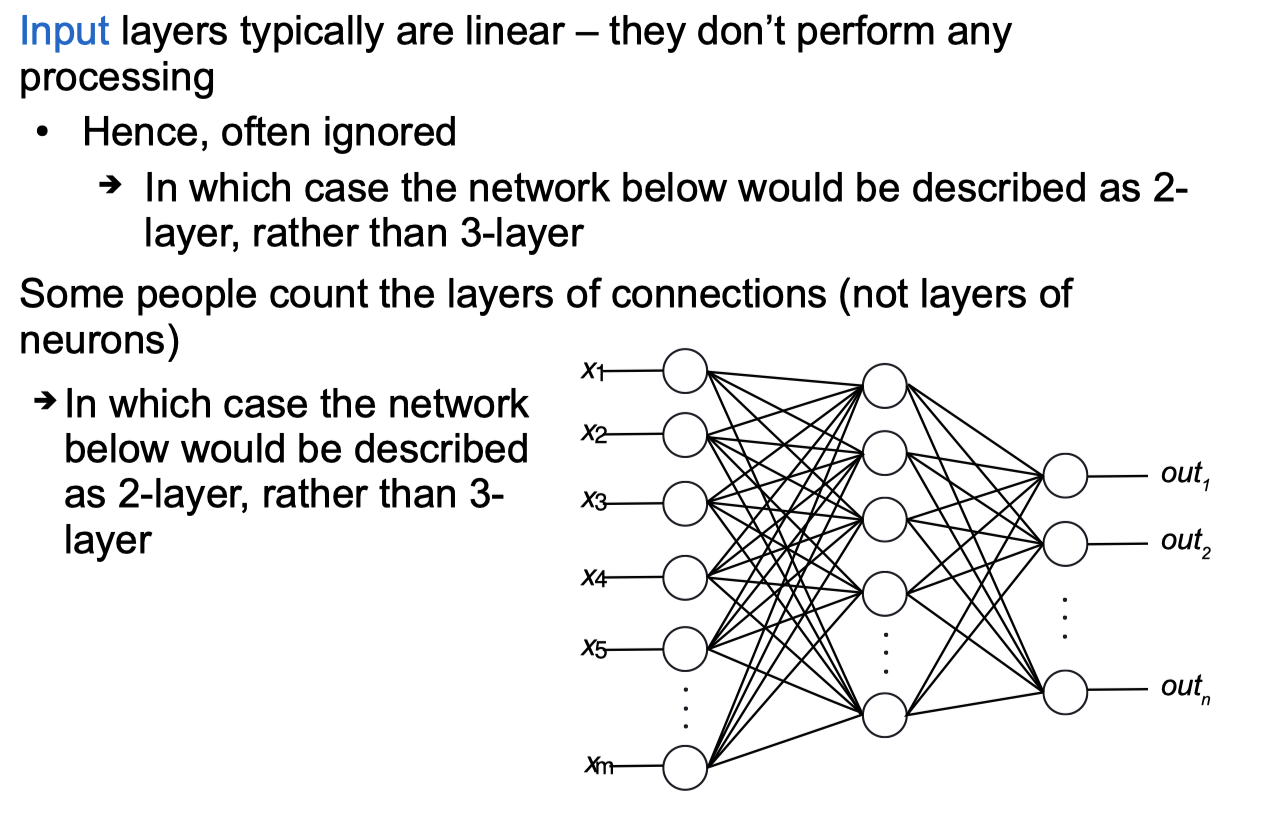
Screen Shot 2022-05-12 at 13.20.04.png

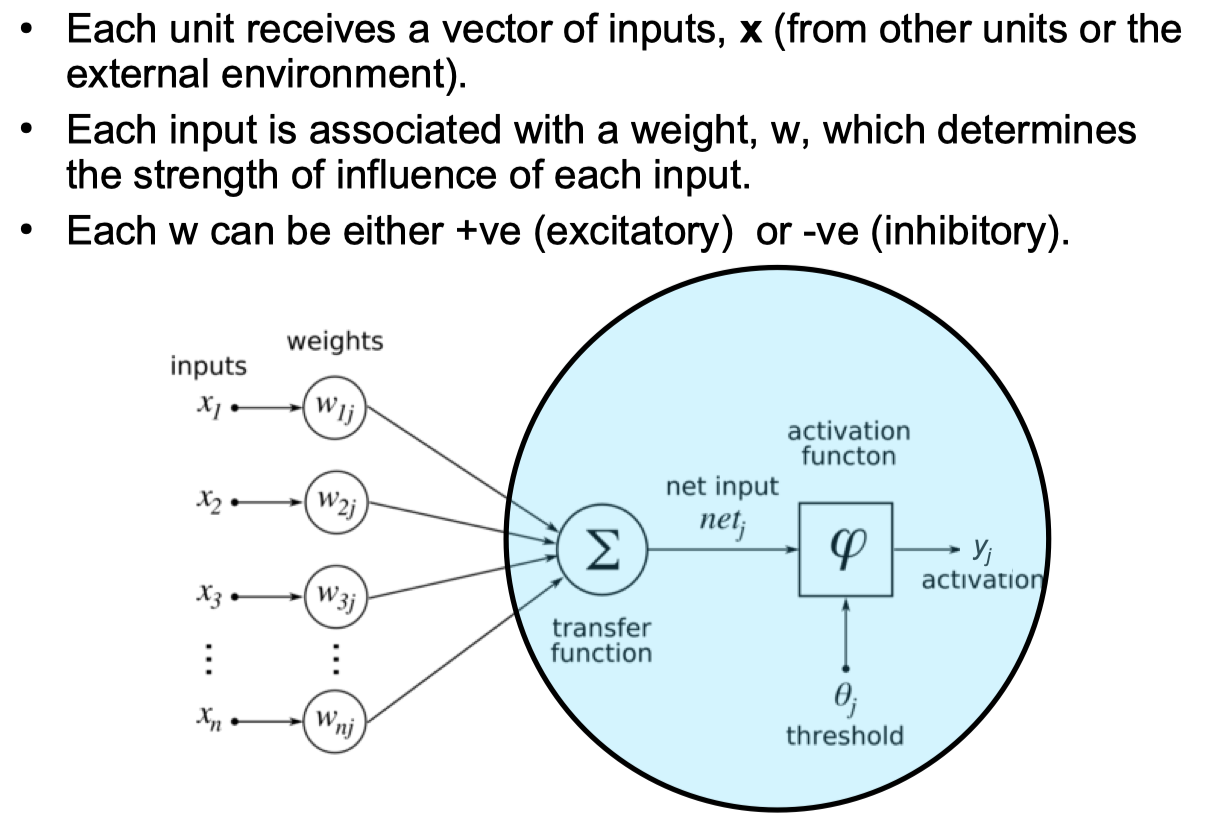
Screen Shot 2022-05-12 at 13.20.16.png

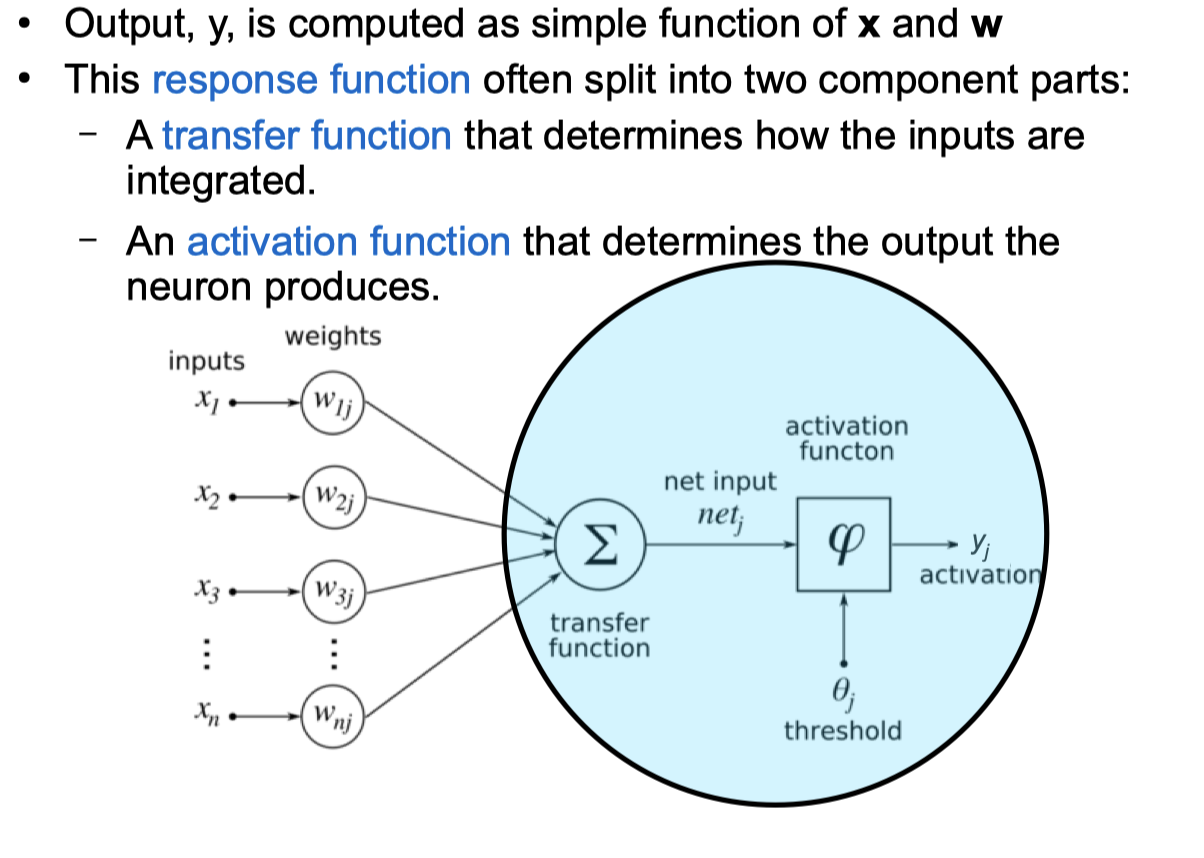
Screen Shot 2022-05-12 at 13.20.39.png

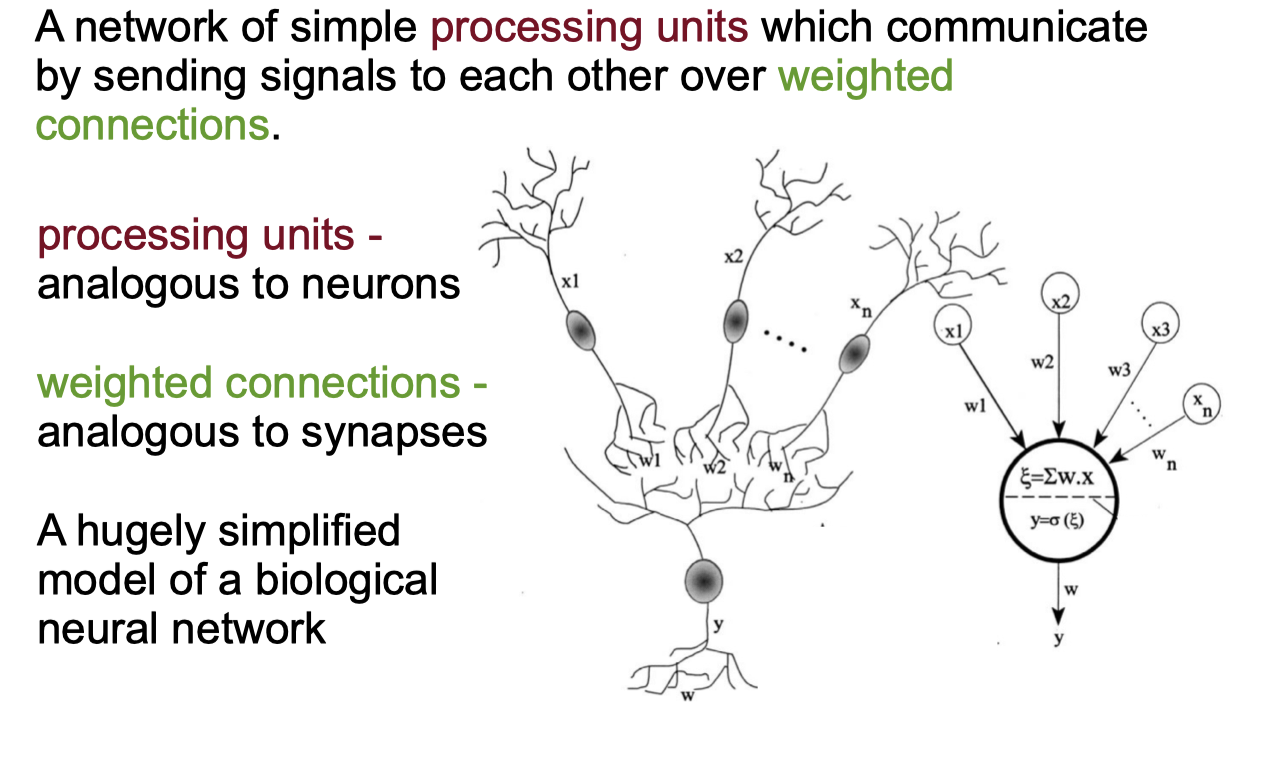
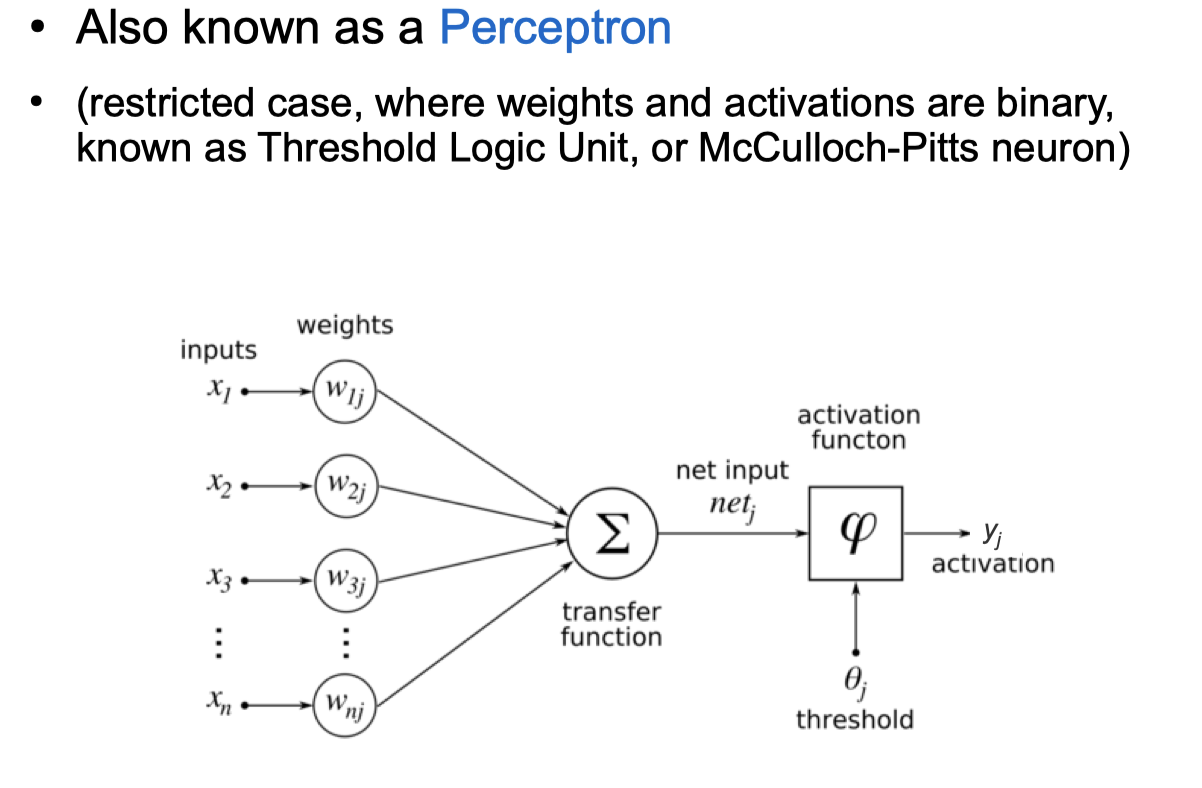
Linear Threshold Unit / Perceptron

Screen Shot 2022-05-12 at 14.08.05.png

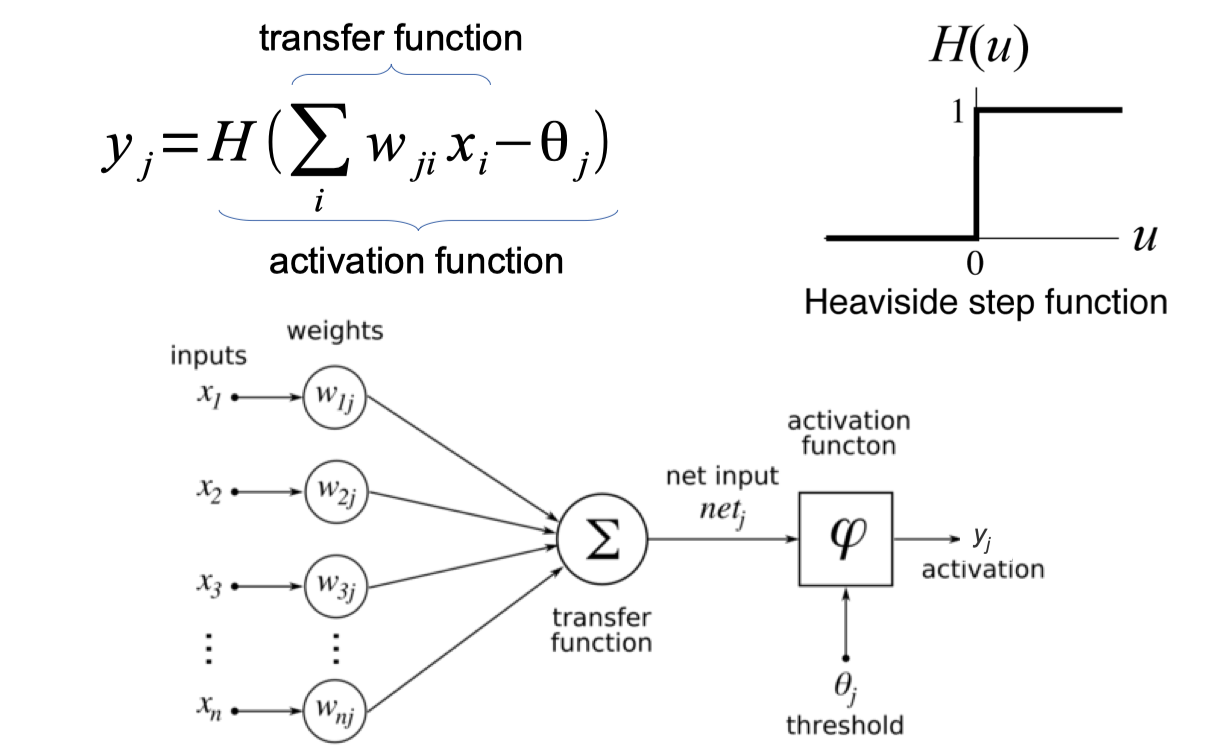
Screen Shot 2022-05-12 at 14.08.19.png

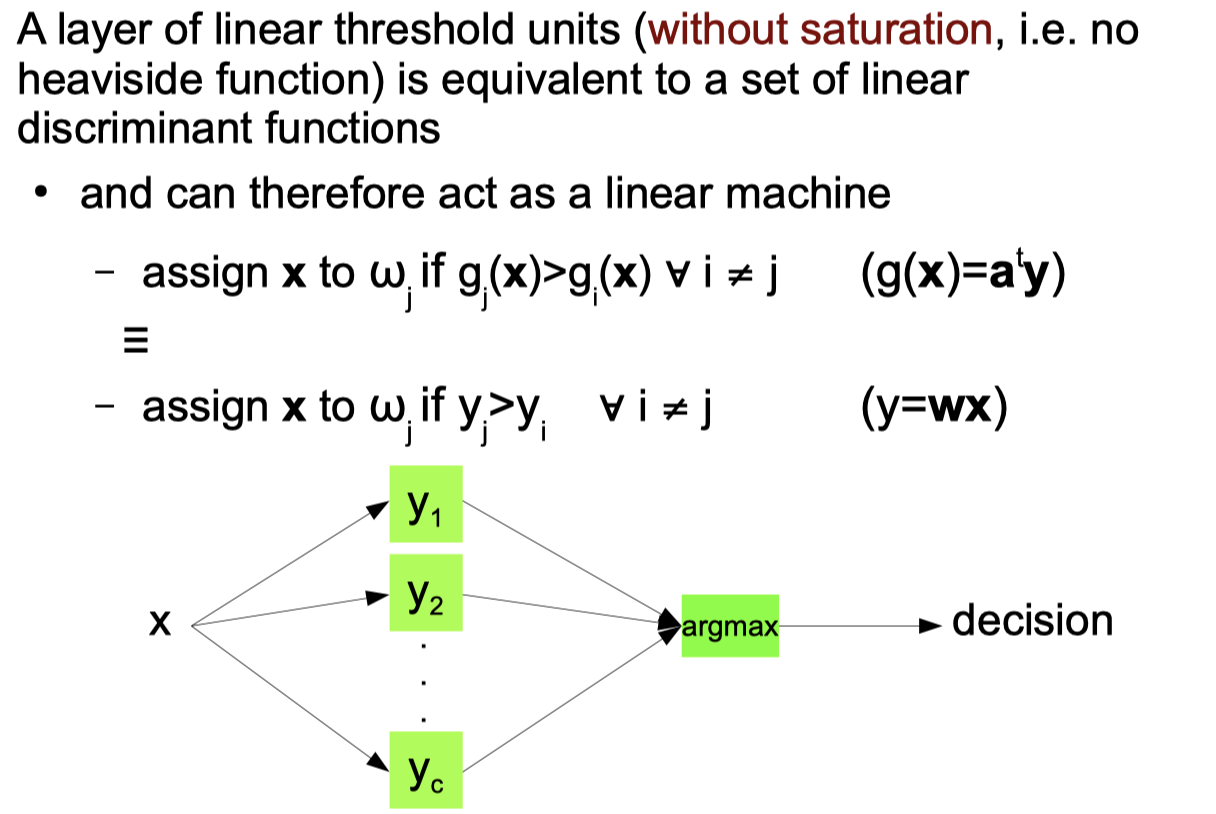
Screen Shot 2022-05-12 at 14.08.48.png

Screen Shot 2022-05-12 at 14.08.58.png

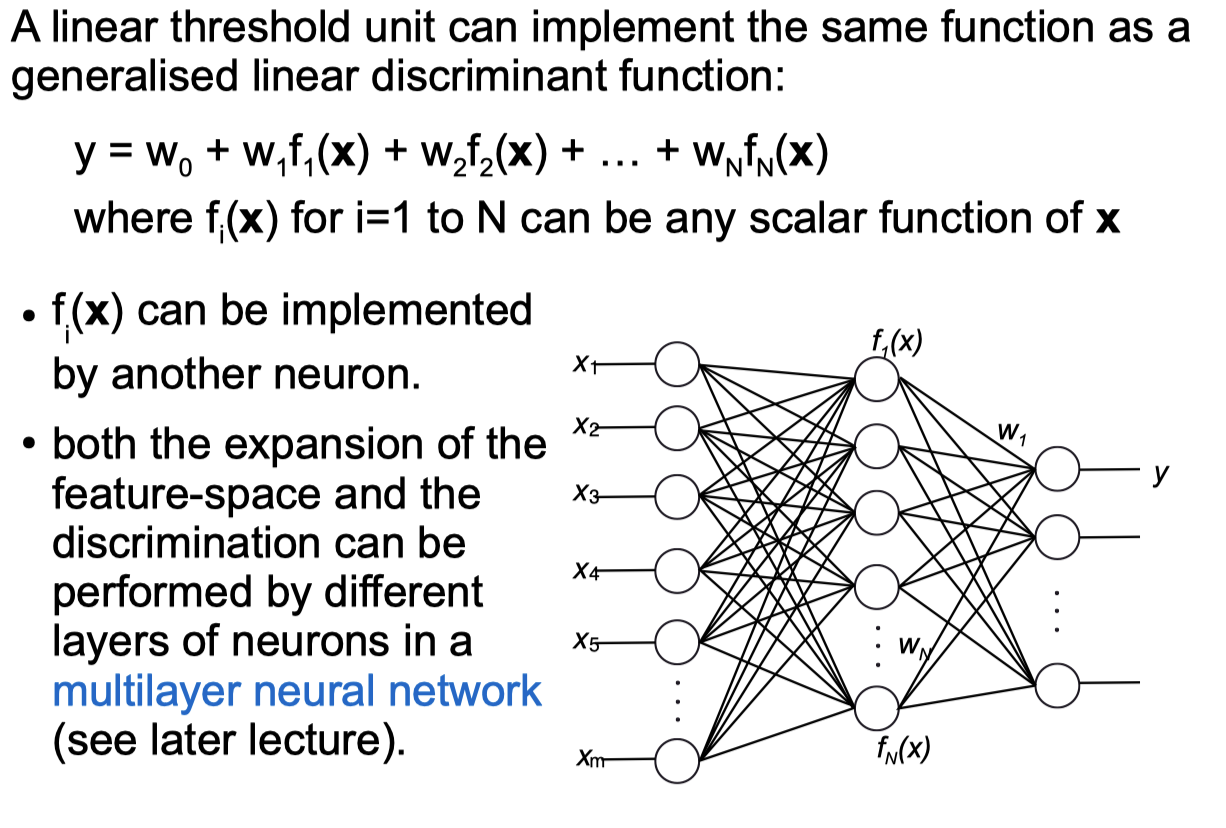
Screen Shot 2022-05-12 at 14.11.54.png

Linear Threshold Unit Python code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# Linear Threshold Unit
def h_func(x):
    if x < 0:
        return 0
    else:
        return 1

x = [[0,0],[0,1],[1,0],[1,1]]
# logical AND
b = 1.5
# w = np.ones(len(x))
# logical NOT
# b = -0.5
# w = np.ones(len(x)) * (-1)
# logical OR
# b = 0.5
# w = np.ones(len(x))


# define w
w = [1,1]


result = []
for sample in x:
    temp = np.dot(w,sample) - b
    y = h_func(temp)
    result.append((sample,np.dot(w,sample),temp,y))

pt = PrettyTable(('Sample','wx','wx-b','h(wx-b)'))
for row in result: pt.add_row(row)
print(pt)

Output

1
2
3
4
5
6
7
8

+--------+----+------+---------+
| Sample | wx | wx-b | h(wx-b) |
+--------+----+------+---------+
| [0, 0] | 0  | -1.5 |    0    |
| [0, 1] | 1  | -0.5 |    0    |
| [1, 0] | 1  | -0.5 |    0    |
| [1, 1] | 2  | 0.5  |    1    |
+--------+----+------+---------+

Delta Learning Rule

Screen Shot 2022-05-12 at 14.13.14.png

Delta Learning Rule Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

# Delta Learning Rule
import numpy as np
from prettytable import PrettyTable

# configuration variables
# -----------------------------------------------------------
# initial values
# w = [b,w0,w1]
# H(wx - theta)
# w = [-theta,w0,w1]
theta = 1.5
w = [-theta,5,-1]

# learning rate
n = 1

def H(input):
    if input < 0:
        return 0
    else:
        return 1

# iterations
# iterations = 150
epoch = 3
# dataset
# -----------------------------------------------------------
X = [[0,0],[1,0],[2,1],[0,1],[1,2]]
Y = [1,1,1,0,0]

# sequential widrow-hoff learning algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
    for i in range(len(Y)):
        w_prev = w
        x = np.hstack((np.array(1),X[i]))
        y = Y[i]

        # calculate wx
        wx = np.dot(w, x)

        # calculate update part
        temp =  H(wx)
        update = n * (y - H(wx)) * x

        # add update part to a
        w = np.add(w, update)

        cur_result = []
        # evaluate
        for index in range(len(Y)):
            y_1 = np.hstack((1,X[index]))
            cur_result.append(H(np.dot(w, y_1)))

        # check if converage
        is_converage = True
        for index in range(len(Y)):
            if cur_result[index] != Y[index]:
                is_converage = False
                
        # append result
        result.append((str(i + 1 + (len(Y) * o)),x, np.round(w_prev, 4), np.round(y, 4), np.round(wx, 4),y,temp,update, np.round(w, 4),np.round(cur_result, 4),is_converage))

# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration','x', 'w', 't', 'wx','y = h(wx)','t-y','η(t-y)x', 'w_new = w + η(t - y)x','over all result','is converage'))
for row in result: pt.add_row(row)
print(pt)

Output

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

+-----------+---------+------------------+---+------+-----------+-----+------------+-----------------------+-----------------+--------------+
| iteration |    x    |        w         | t |  wx  | y = h(wx) | t-y |  η(t-y)x   | w_new = w + η(t - y)x | over all result | is converage |
+-----------+---------+------------------+---+------+-----------+-----+------------+-----------------------+-----------------+--------------+
|     1     | [1 0 0] | [-1.5  5.  -1. ] | 1 | -1.5 |     1     |  0  |  [1 0 0]   |    [-0.5  5.  -1. ]   |   [0 1 1 0 1]   |    False     |
|     2     | [1 1 0] | [-0.5  5.  -1. ] | 1 | 4.5  |     1     |  1  |  [0 0 0]   |    [-0.5  5.  -1. ]   |   [0 1 1 0 1]   |    False     |
|     3     | [1 2 1] | [-0.5  5.  -1. ] | 1 | 8.5  |     1     |  1  |  [0 0 0]   |    [-0.5  5.  -1. ]   |   [0 1 1 0 1]   |    False     |
|     4     | [1 0 1] | [-0.5  5.  -1. ] | 0 | -1.5 |     0     |  0  |  [0 0 0]   |    [-0.5  5.  -1. ]   |   [0 1 1 0 1]   |    False     |
|     5     | [1 1 2] | [-0.5  5.  -1. ] | 0 | 2.5  |     0     |  1  | [-1 -1 -2] |    [-1.5  4.  -3. ]   |   [0 1 1 0 0]   |    False     |
|     6     | [1 0 0] | [-1.5  4.  -3. ] | 1 | -1.5 |     1     |  0  |  [1 0 0]   |    [-0.5  4.  -3. ]   |   [0 1 1 0 0]   |    False     |
|     7     | [1 1 0] | [-0.5  4.  -3. ] | 1 | 3.5  |     1     |  1  |  [0 0 0]   |    [-0.5  4.  -3. ]   |   [0 1 1 0 0]   |    False     |
|     8     | [1 2 1] | [-0.5  4.  -3. ] | 1 | 4.5  |     1     |  1  |  [0 0 0]   |    [-0.5  4.  -3. ]   |   [0 1 1 0 0]   |    False     |
|     9     | [1 0 1] | [-0.5  4.  -3. ] | 0 | -3.5 |     0     |  0  |  [0 0 0]   |    [-0.5  4.  -3. ]   |   [0 1 1 0 0]   |    False     |
|     10    | [1 1 2] | [-0.5  4.  -3. ] | 0 | -2.5 |     0     |  0  |  [0 0 0]   |    [-0.5  4.  -3. ]   |   [0 1 1 0 0]   |    False     |
|     11    | [1 0 0] | [-0.5  4.  -3. ] | 1 | -0.5 |     1     |  0  |  [1 0 0]   |    [ 0.5  4.  -3. ]   |   [1 1 1 0 0]   |     True     |
|     12    | [1 1 0] | [ 0.5  4.  -3. ] | 1 | 4.5  |     1     |  1  |  [0 0 0]   |    [ 0.5  4.  -3. ]   |   [1 1 1 0 0]   |     True     |
|     13    | [1 2 1] | [ 0.5  4.  -3. ] | 1 | 5.5  |     1     |  1  |  [0 0 0]   |    [ 0.5  4.  -3. ]   |   [1 1 1 0 0]   |     True     |
|     14    | [1 0 1] | [ 0.5  4.  -3. ] | 0 | -2.5 |     0     |  0  |  [0 0 0]   |    [ 0.5  4.  -3. ]   |   [1 1 1 0 0]   |     True     |
|     15    | [1 1 2] | [ 0.5  4.  -3. ] | 0 | -1.5 |     0     |  0  |  [0 0 0]   |    [ 0.5  4.  -3. ]   |   [1 1 1 0 0]   |     True     |
+-----------+---------+------------------+---+------+-----------+-----+------------+-----------------------+-----------------+--------------+

Softmax Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# softmax
import math

y = [0.34,0.73,-0.16]
# β hyperparameter
b = 1

total = 0
for sample in y:
    total += math.exp(sample*b)
result = []
for sample in y:
    result.append((sample,np.round(math.exp(sample*b)/total, 4)))

pt = PrettyTable(('Sample','softmax'))
for row in result: pt.add_row(row)
print(pt)

Output

1
2
3
4
5
6
7

+--------+---------+
| Sample | softmax |
+--------+---------+
|  0.34  |  0.3243 |
|  0.73  |  0.479  |
| -0.16  |  0.1967 |
+--------+---------+

Hebbian Learning Rule

Screen Shot 2022-05-12 at 14.45.06.png

Competitive Learning Networks

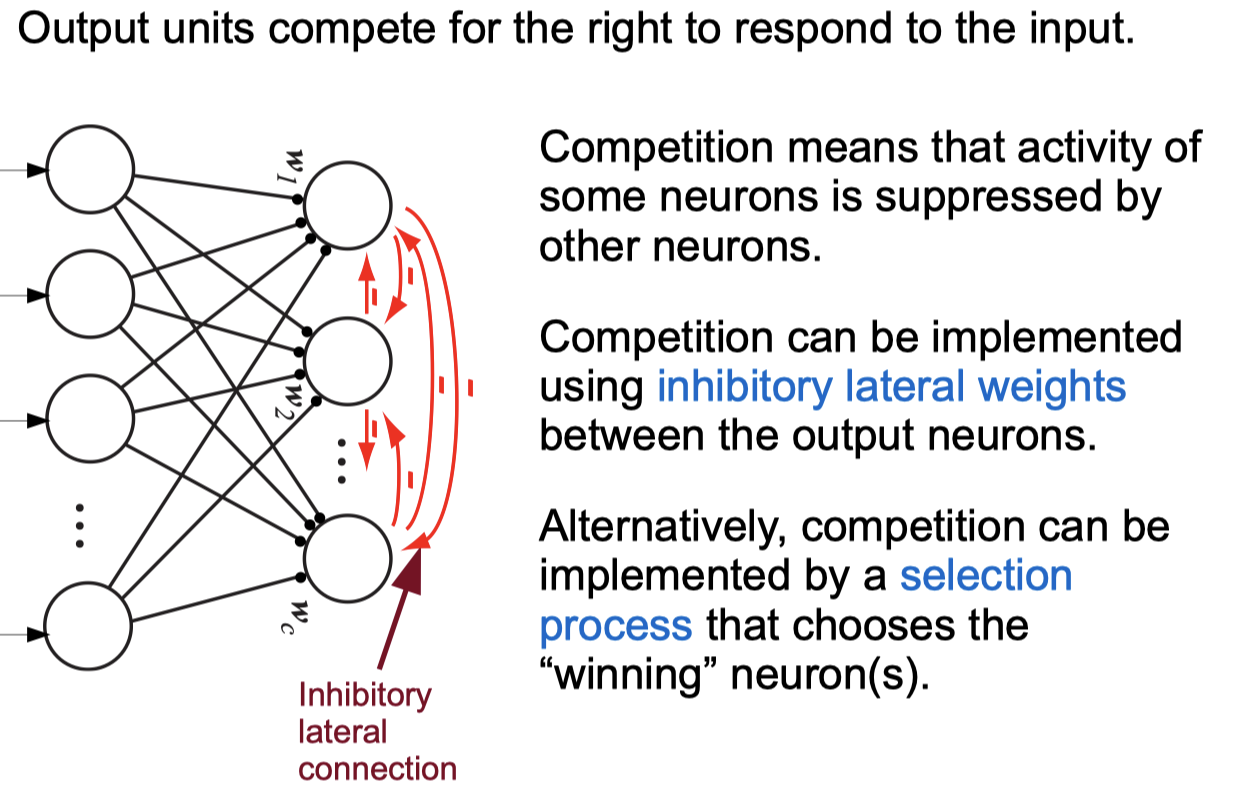
Screen Shot 2022-05-12 at 14.45.39.png

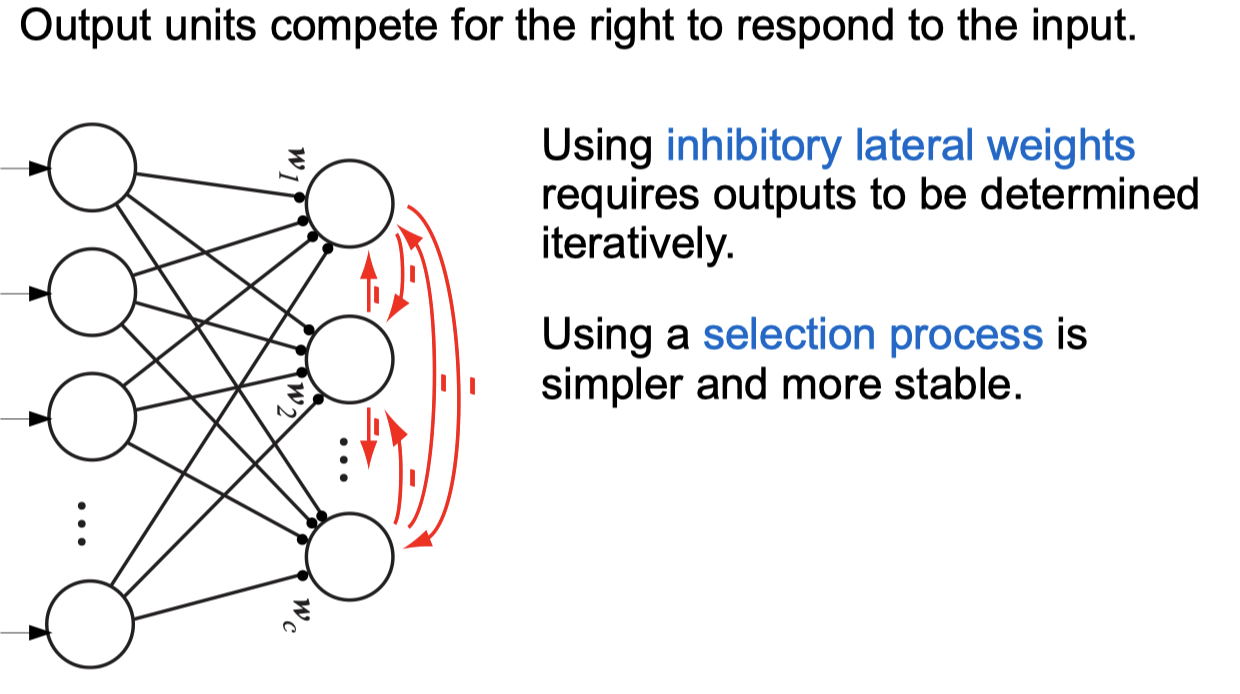
Screen Shot 2022-05-12 at 14.45.56.png

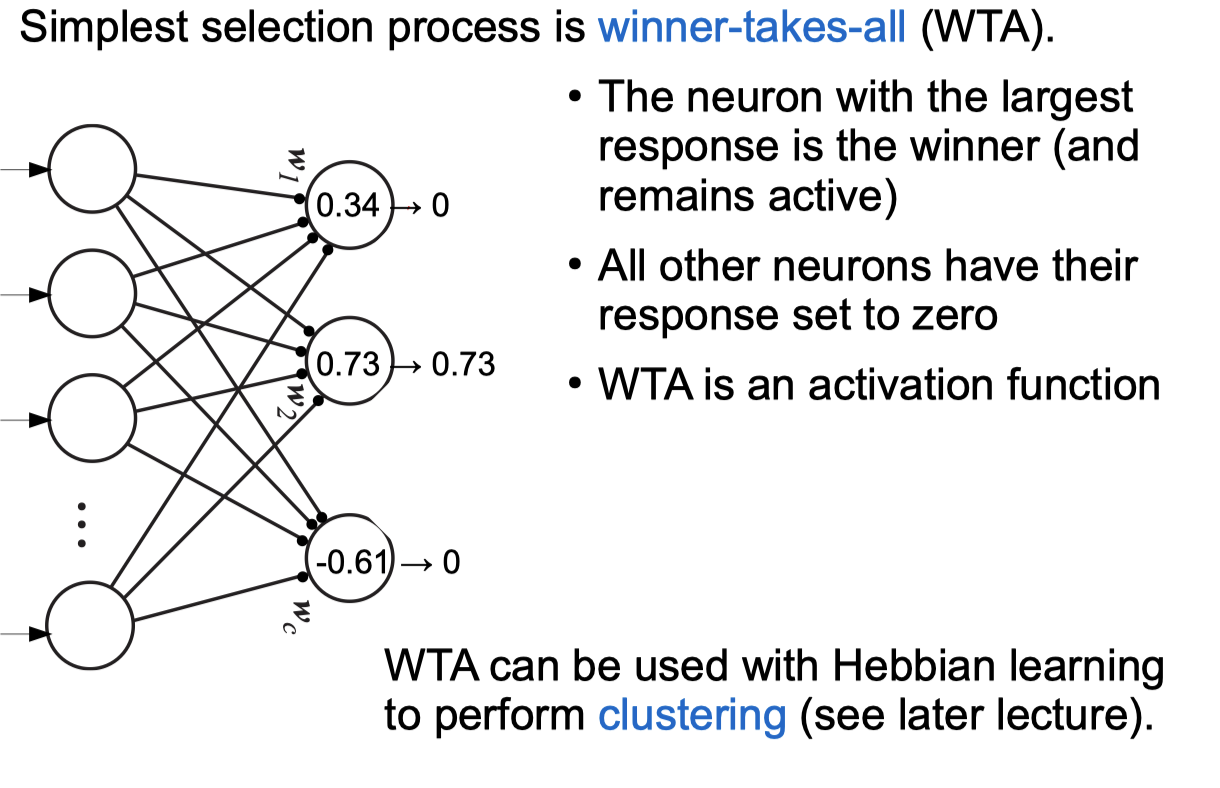
Screen Shot 2022-05-12 at 14.46.11.png

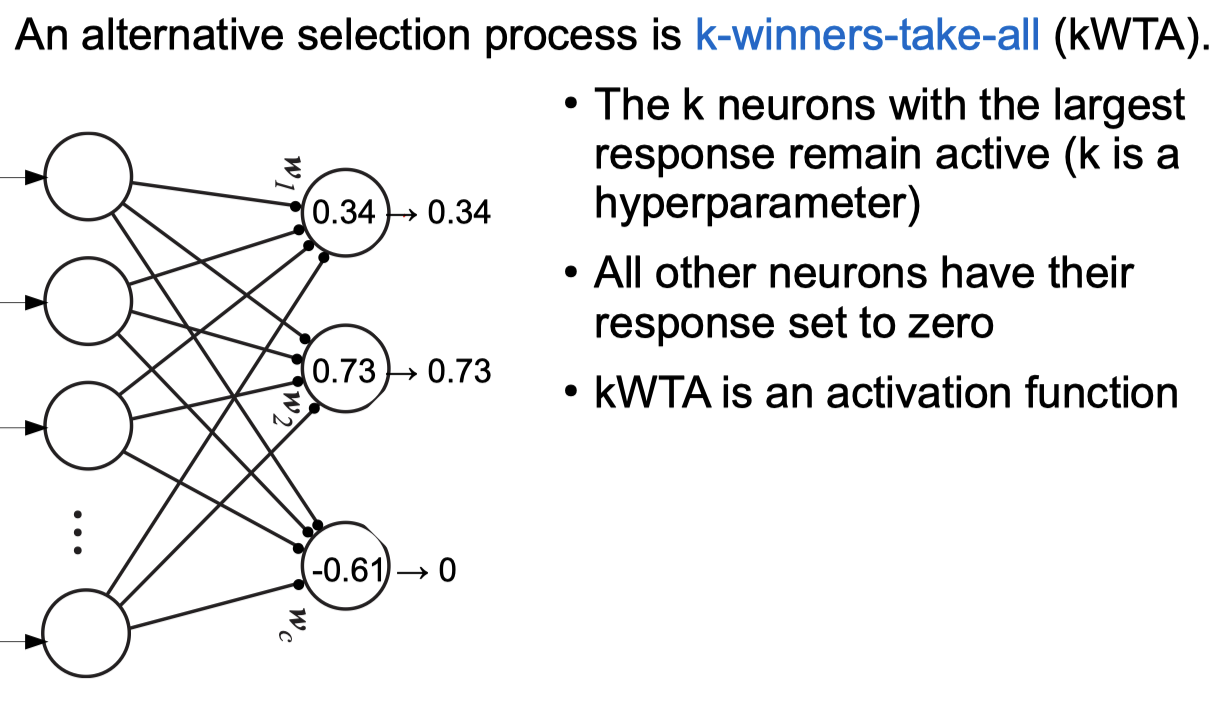
Screen Shot 2022-05-12 at 14.46.21.png

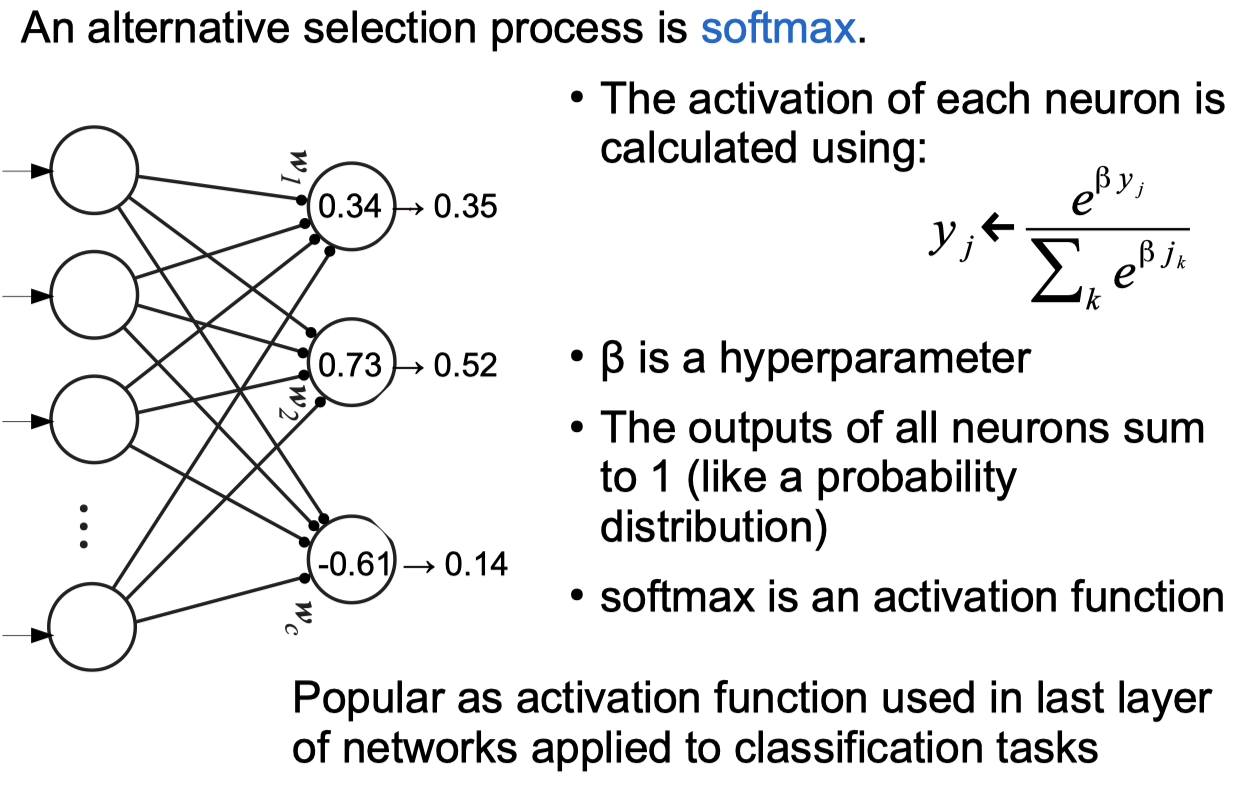
Screen Shot 2022-05-12 at 14.46.34.png

Negative Feedback Networks

Screen Shot 2022-05-12 at 15.00.14.png

Screen Shot 2022-05-12 at 15.00.24.png

Negative feedback network Python code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# negative feedback network
from prettytable import PrettyTable
from fractions import Fraction
# w and x stay unchange
w = [[1,1,0],[1,1,1]]
x = [1,1,0]
y = [0,0]
# parameter α = 0.25
b = 0.25
iternation = 10
result = []
for i in range(iternation):
    w_prev = w
    wy = np.dot(np.transpose(w),y)
    e = x - wy
    we = np.dot(w,e)
    y = y + b*we
    # append result
    result.append((str(i + 1),y,np.round(wy,4), np.round(e, 4), np.round(we, 4),np.round(y,4)))

pt = PrettyTable(('iteration','y','wy_new','e=x-wy','we','y_new = y + b*we'))
for row in result: pt.add_row(row)
print(pt)

Output

1
2
3
4
5
6
7
8
9
10
11
12
13
14

+-----------+-------------------------+------------------------+---------------------------+-------------------+------------------+
| iteration |            y            |         wy_new         |           e=x-wy          |         we        | y_new = y + b*we |
+-----------+-------------------------+------------------------+---------------------------+-------------------+------------------+
|     1     |        [0.5 0.5]        |        [0 0 0]         |          [1 1 0]          |       [2 2]       |    [0.5 0.5]     |
|     2     |      [0.5   0.375]      |     [1.  1.  0.5]      |      [ 0.   0.  -0.5]     |    [ 0.  -0.5]    |  [0.5   0.375]   |
|     3     |    [0.5625  0.34375]    |  [0.875 0.875 0.375]   |   [ 0.125  0.125 -0.375]  |  [ 0.25  -0.125]  | [0.5625 0.3438]  |
|     4     |  [0.609375  0.3046875]  | [0.9062 0.9062 0.3438] | [ 0.0938  0.0938 -0.3438] | [ 0.1875 -0.1562] | [0.6094 0.3047]  |
|     5     | [0.65234375 0.27148438] | [0.9141 0.9141 0.3047] | [ 0.0859  0.0859 -0.3047] | [ 0.1719 -0.1328] | [0.6523 0.2715]  |
|     6     | [0.69042969 0.24169922] | [0.9238 0.9238 0.2715] | [ 0.0762  0.0762 -0.2715] | [ 0.1523 -0.1191] | [0.6904 0.2417]  |
|     7     | [0.72436523 0.21520996] | [0.9321 0.9321 0.2417] | [ 0.0679  0.0679 -0.2417] | [ 0.1357 -0.106 ] | [0.7244 0.2152]  |
|     8     | [0.75457764 0.19161987] | [0.9396 0.9396 0.2152] | [ 0.0604  0.0604 -0.2152] | [ 0.1208 -0.0944] | [0.7546 0.1916]  |
|     9     | [0.78147888 0.17061615] | [0.9462 0.9462 0.1916] | [ 0.0538  0.0538 -0.1916] | [ 0.1076 -0.084 ] | [0.7815 0.1706]  |
|     10    | [0.80543137 0.1519146 ] | [0.9521 0.9521 0.1706] | [ 0.0479  0.0479 -0.1706] | [ 0.0958 -0.0748] | [0.8054 0.1519]  |
+-----------+-------------------------+------------------------+---------------------------+-------------------+------------------+

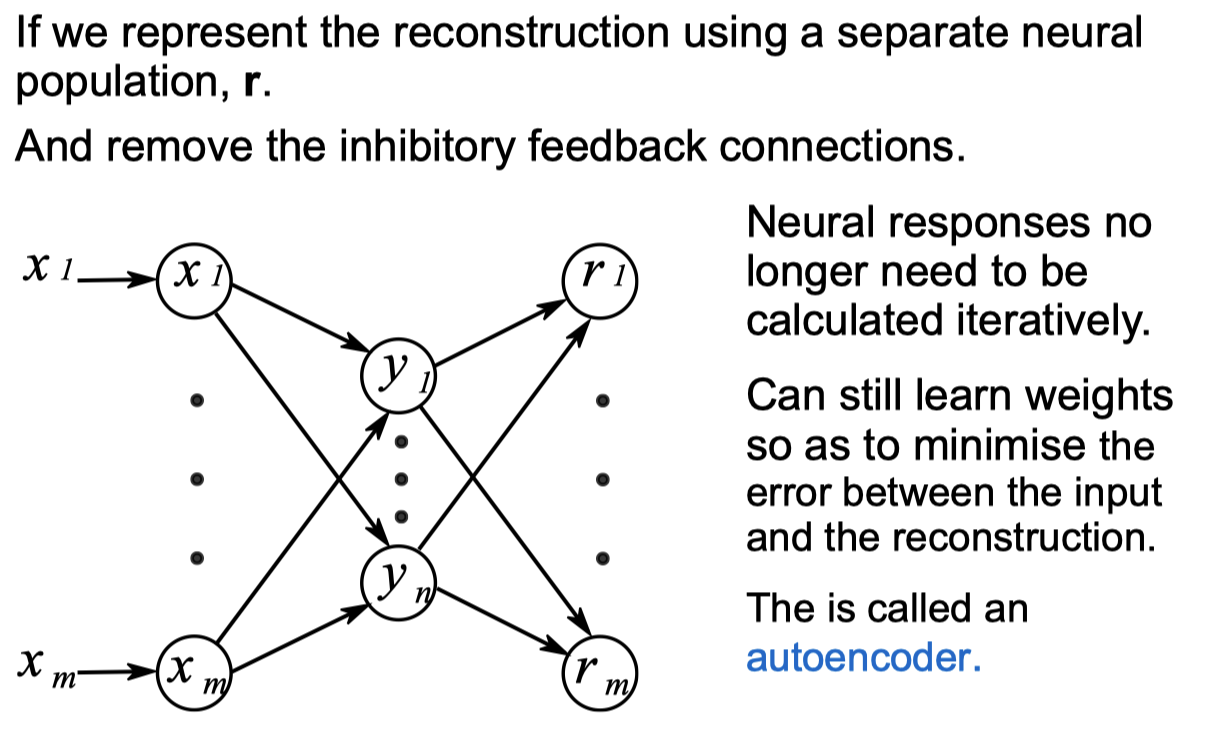
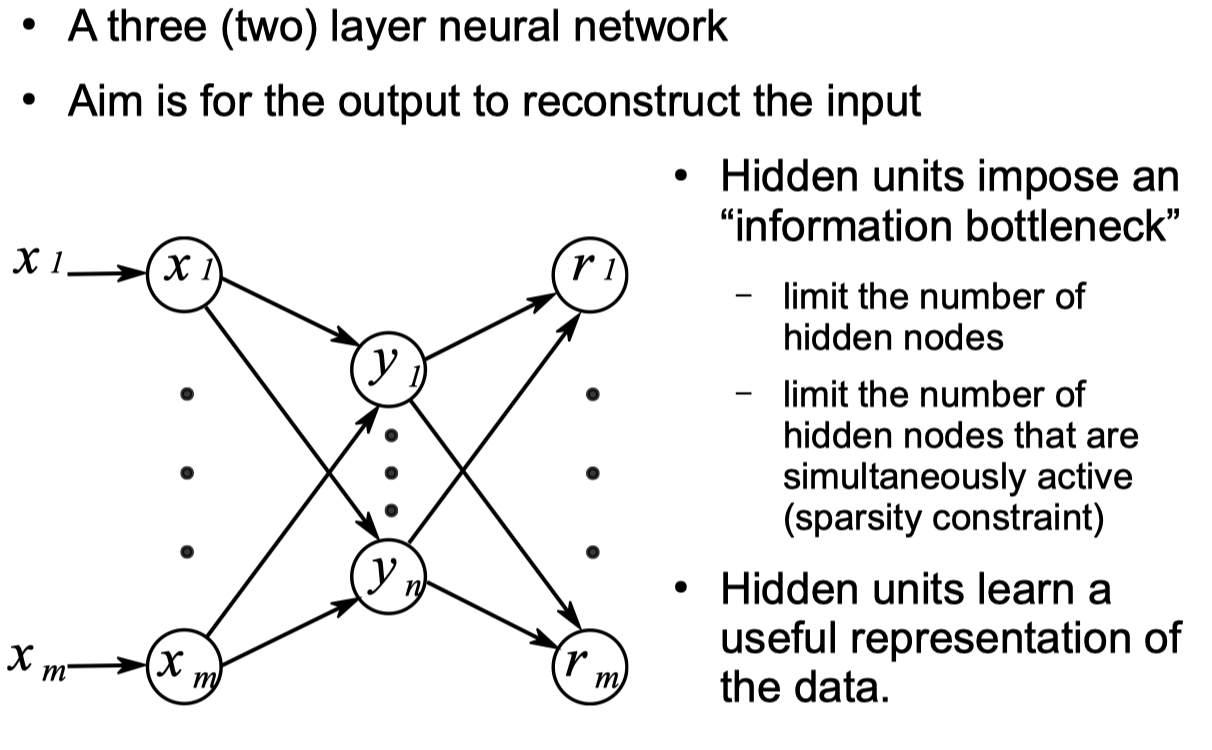
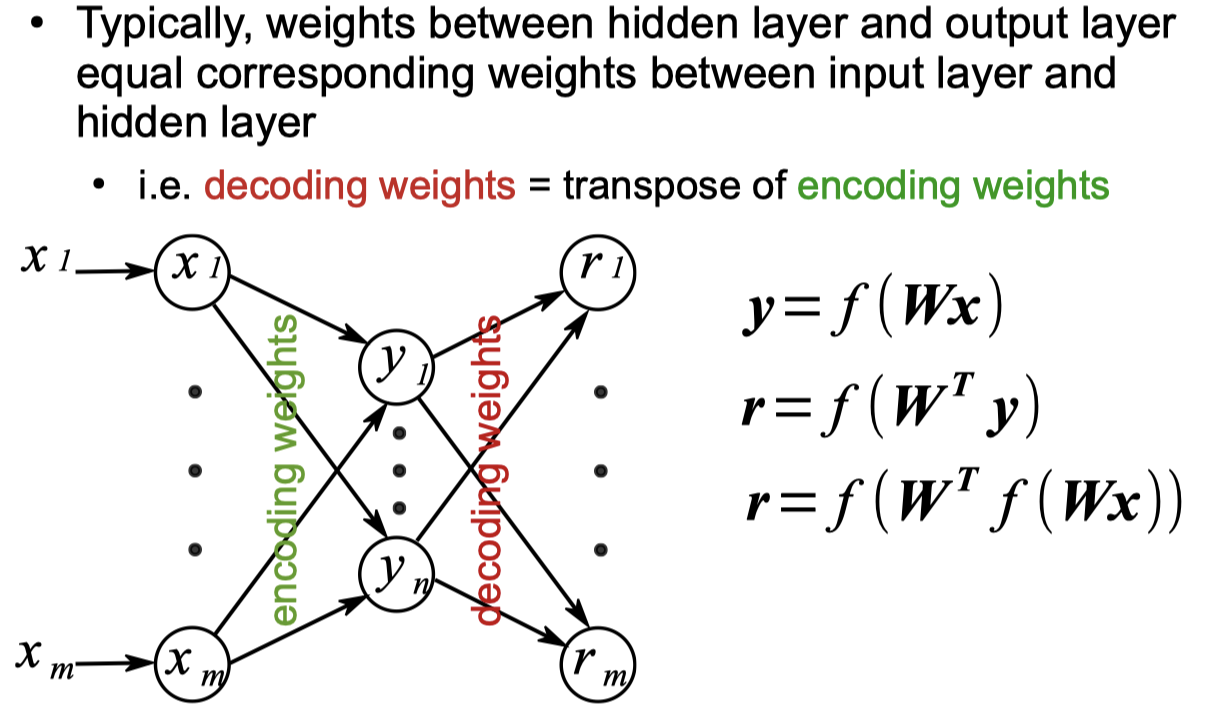
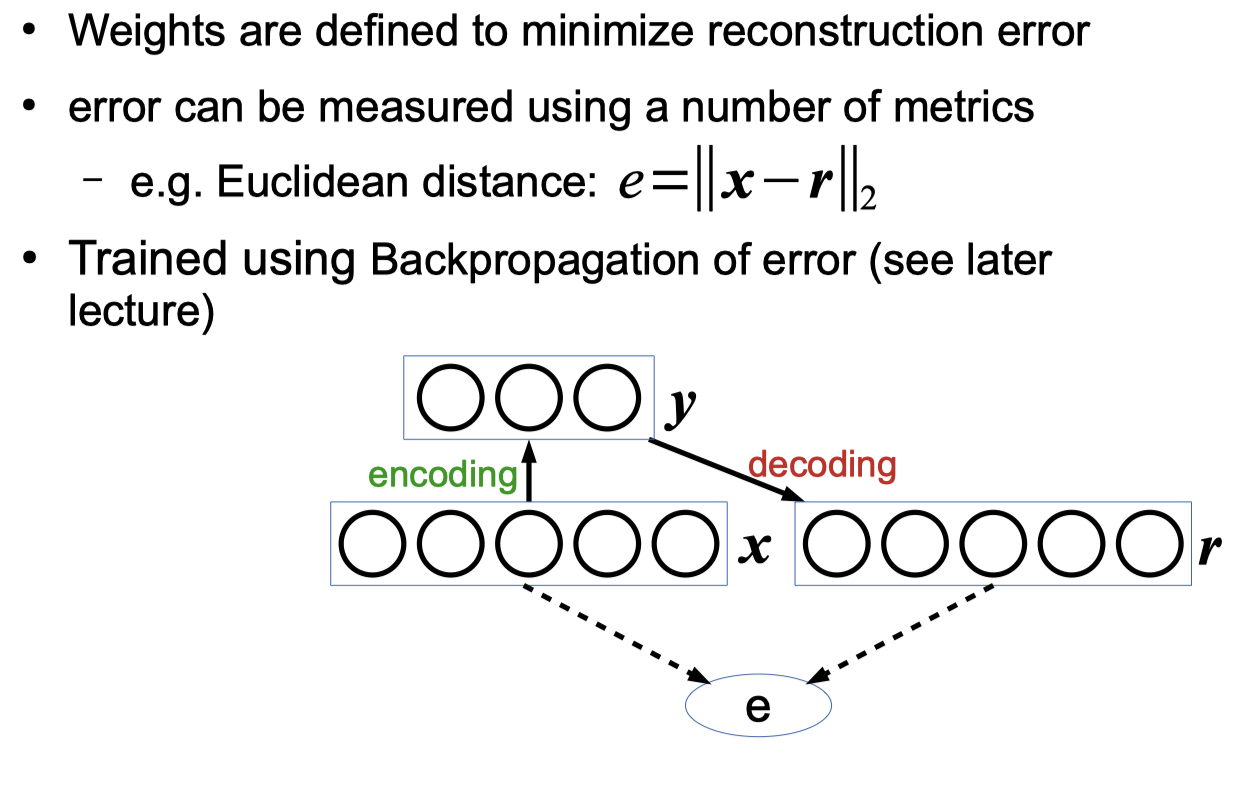
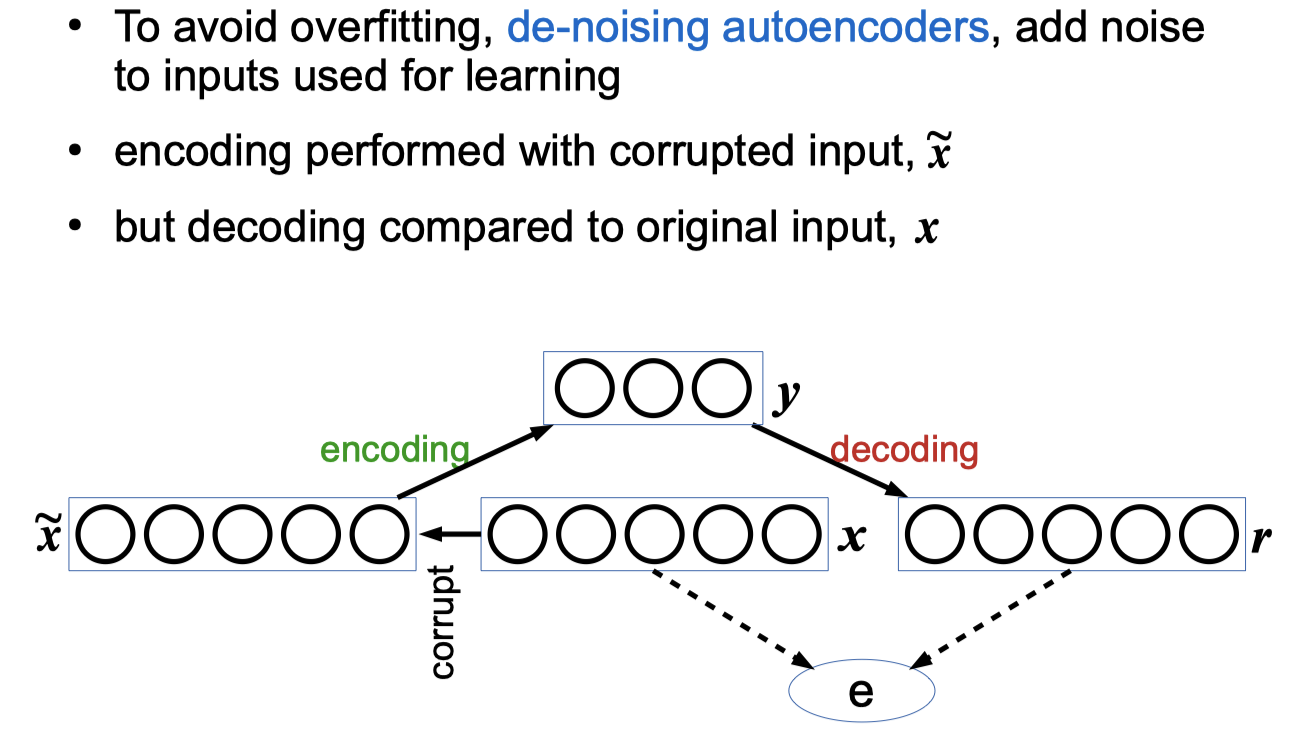
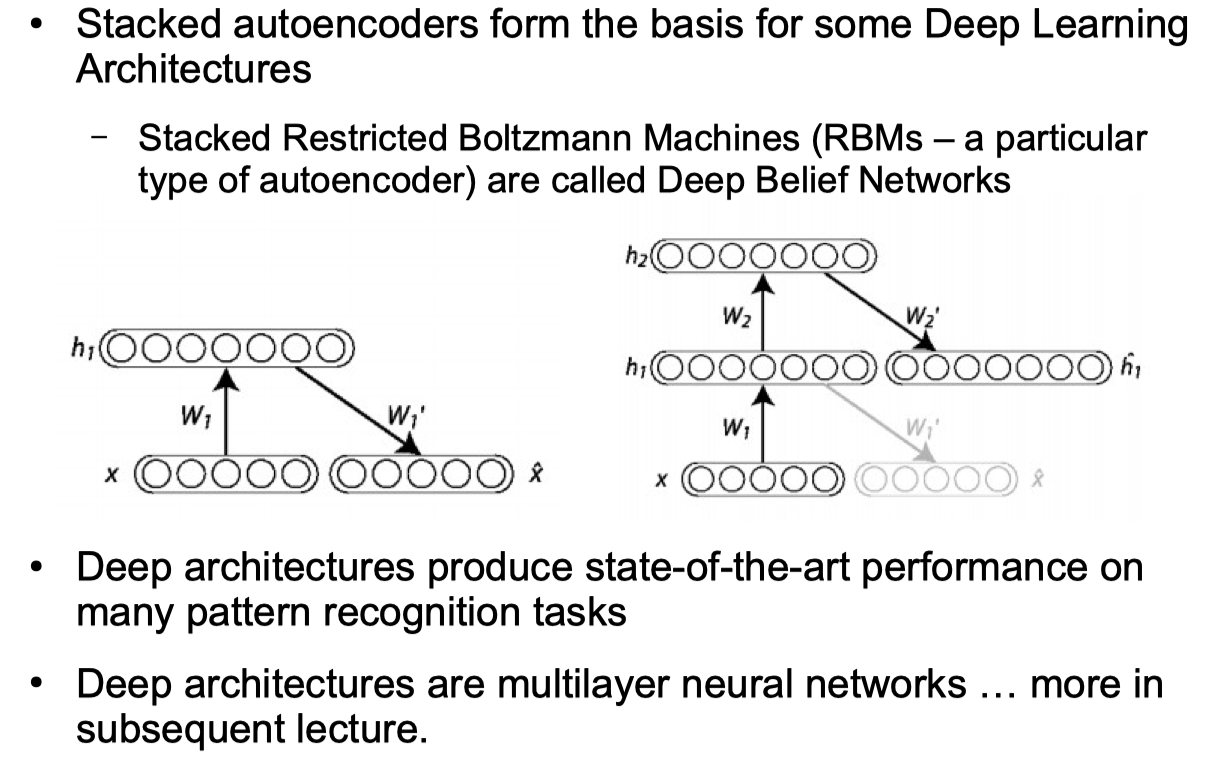
Autoencoder Networks

Screen Shot 2022-05-12 at 15.00.49.png

Screen Shot 2022-05-12 at 15.01.20.png

Screen Shot 2022-05-12 at 15.01.36.png

Screen Shot 2022-05-12 at 15.01.52.png

Screen Shot 2022-05-12 at 15.02.04.png

Screen Shot 2022-05-12 at 15.02.16.png

Deep Learning, Neural Networks
Deep Learning Neural Networks python code tutorial
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

Discriminant Functions

Multilayer Perceptrons and Backpropagation

Comments powered by Disqus.