Deep Learning: Discriminant Functions
Here is my Deep Learning Full Tutorial!
Discriminant functions divide feature space into regions
Linear Discriminant Functions

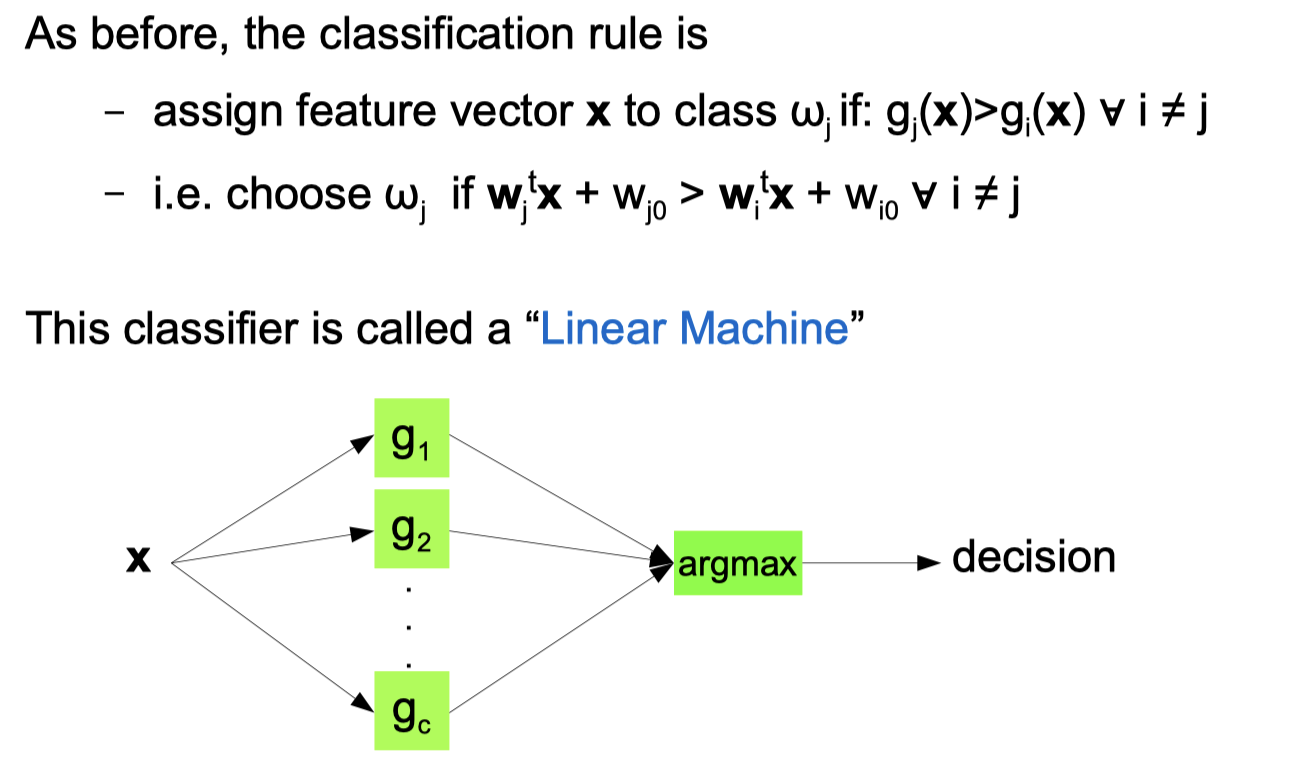
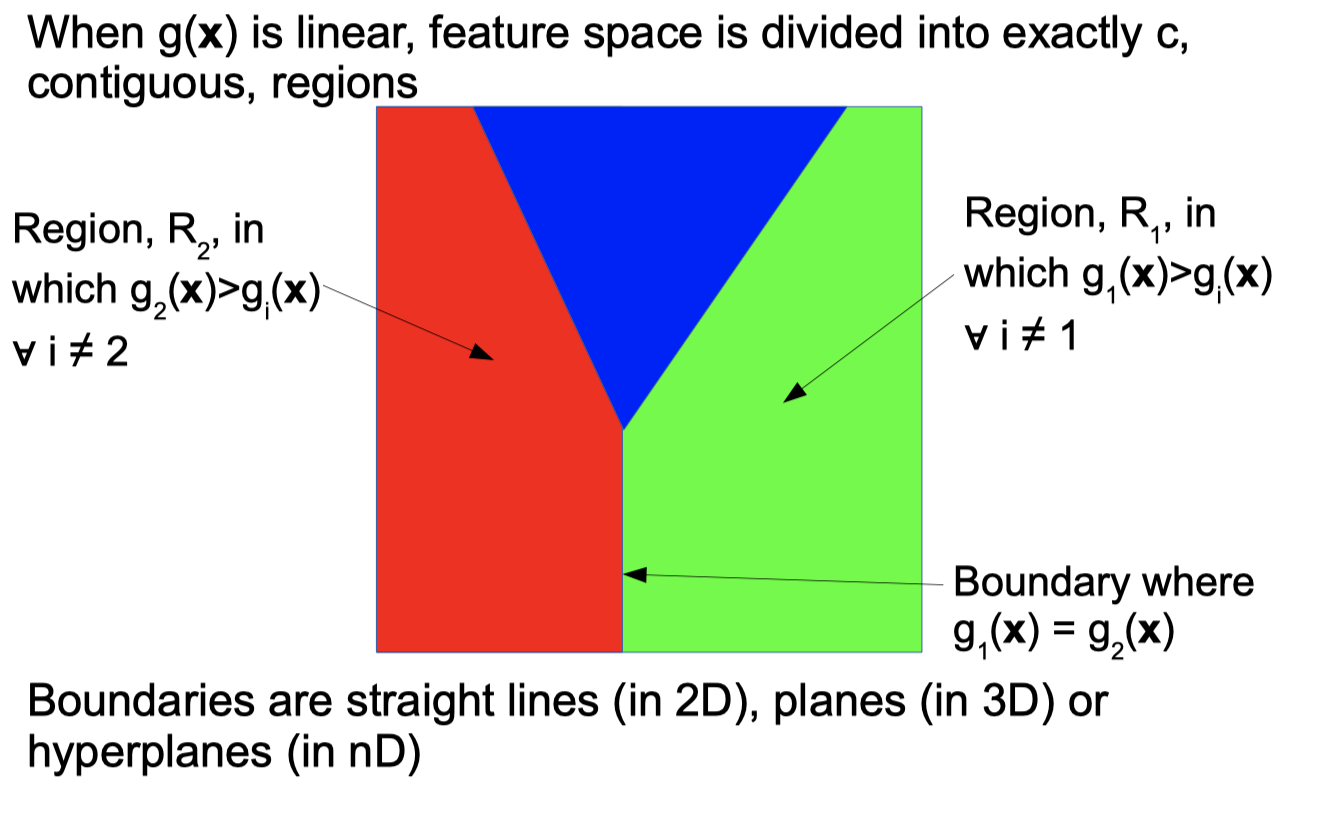


Generalised Linear Discriminant Functions

Dichotomizer Python code
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
X = [
[1,1],
[2,2],
[3,3]
]
w = [2,1]
b = -5
def g(w,x,b):
return np.dot(w,x) + b
result = [g(w,x,b) for x in X]
print(result)
Output
1
[-2, 1, 4]
Learning Decision Boundaries
perceptron learning
Perceptron Criterion Function
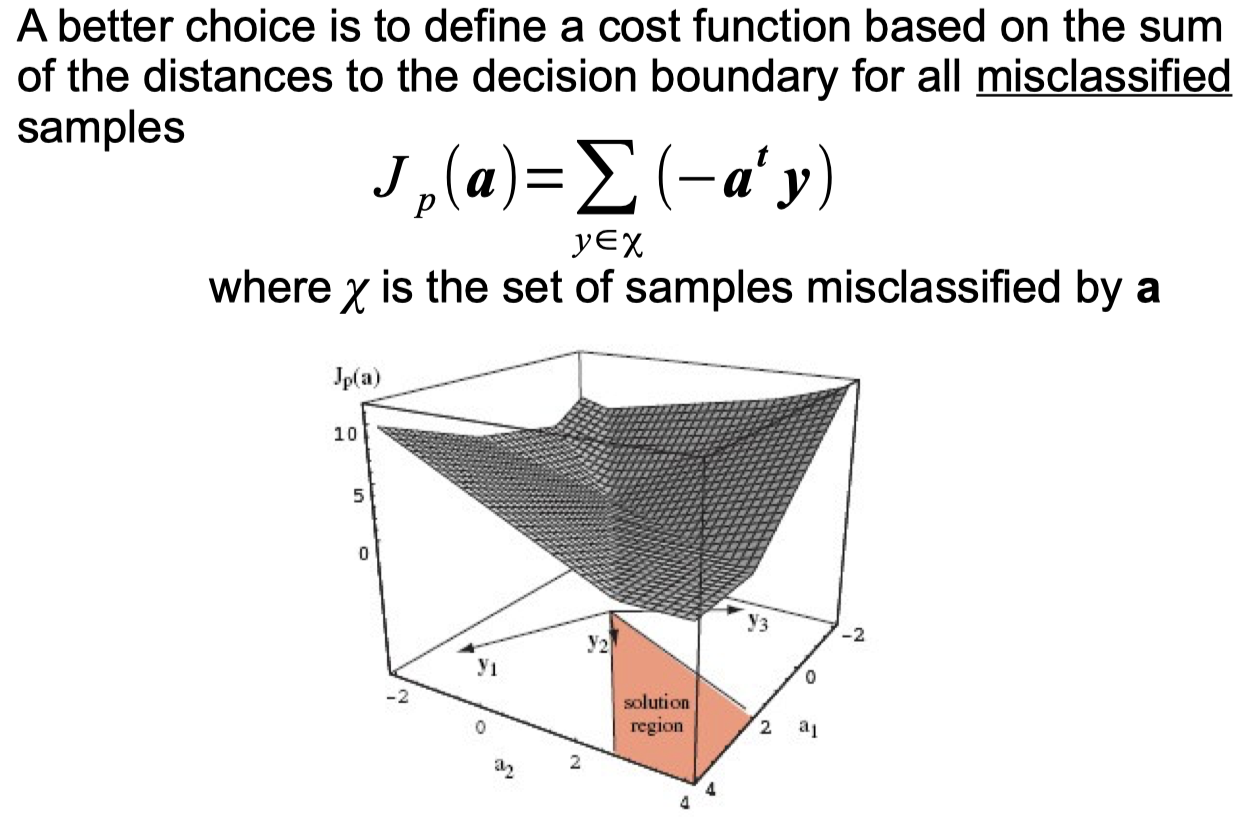


Sequential Perceptron Learning Algorithm




Sequential Perceptron Learning Algorithm Python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# Sequential Perceptron Learning Algorithm
import numpy as np
from prettytable import PrettyTable
# configuration variables
# -----------------------------------------------------------
# initial values
# a = [b, w1, w2]
a = [-1.5,5,-1]
# learning rate
n = 1
epoch = 3
# dataset
# -----------------------------------------------------------
X = [[0,0],[1,0],[2,1],[0,1],[1,2]]
Y = [1,1,1,-1,-1]
# Sequential Perceptron Learning Algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
for i in range(len(Y)):
a_prev = a
# y = [1, x1, x2]
y = np.hstack((1,X[i]))
# calculate ay like wx+b = b + w1x1 + w2x2
ay = np.dot(a, y)
#update part ηω'yk
if ay * Y[i] < 0:
if ay > 0:
update = n * y * (-1)
if ay < 0:
update = n * y
# add update part to a
a = np.add(a, update)
cur_result = []
# evaluate
for index in range(len(Y)):
cur_result.append((np.dot(np.hstack((1,X[index])),a)))
# check if converage
is_converage = True
for index in range(len(Y)):
if cur_result[index] * Y[index] <= 0:
is_converage = False
# append result
result.append((str(i + 1 + (len(Y) * o)), np.round(a_prev, 4), np.round(y, 4), np.round(ay, 4), np.round(a, 4),np.round(cur_result, 4),is_converage))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration', 'a', 'y', 'ay', 'a_new','over all result','is converage'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
+-----------+------------------+---------+------+------------------+----------------------------+-------------+
| iteration | a | y | ay | a_new | over all result | is converge |
+-----------+------------------+---------+------+------------------+----------------------------+-------------+
| 1 | [-1.5 5. -1. ] | [1 0 0] | -1.5 | [-0.5 5. -1. ] | [-0.5 4.5 8.5 -1.5 2.5] | False |
| 2 | [-0.5 5. -1. ] | [1 1 0] | 4.5 | [-0.5 5. -1. ] | [-0.5 4.5 8.5 -1.5 2.5] | False |
| 3 | [-0.5 5. -1. ] | [1 2 1] | 8.5 | [-0.5 5. -1. ] | [-0.5 4.5 8.5 -1.5 2.5] | False |
| 4 | [-0.5 5. -1. ] | [1 0 1] | -1.5 | [-0.5 5. -1. ] | [-0.5 4.5 8.5 -1.5 2.5] | False |
| 5 | [-0.5 5. -1. ] | [1 1 2] | 2.5 | [-1.5 4. -3. ] | [-1.5 2.5 3.5 -4.5 -3.5] | False |
| 6 | [-1.5 4. -3. ] | [1 0 0] | -1.5 | [-0.5 4. -3. ] | [-0.5 3.5 4.5 -3.5 -2.5] | False |
| 7 | [-0.5 4. -3. ] | [1 1 0] | 3.5 | [-0.5 4. -3. ] | [-0.5 3.5 4.5 -3.5 -2.5] | False |
| 8 | [-0.5 4. -3. ] | [1 2 1] | 4.5 | [-0.5 4. -3. ] | [-0.5 3.5 4.5 -3.5 -2.5] | False |
| 9 | [-0.5 4. -3. ] | [1 0 1] | -3.5 | [-0.5 4. -3. ] | [-0.5 3.5 4.5 -3.5 -2.5] | False |
| 10 | [-0.5 4. -3. ] | [1 1 2] | -2.5 | [-0.5 4. -3. ] | [-0.5 3.5 4.5 -3.5 -2.5] | False |
| 11 | [-0.5 4. -3. ] | [1 0 0] | -0.5 | [ 0.5 4. -3. ] | [ 0.5 4.5 5.5 -2.5 -1.5] | True |
| 12 | [ 0.5 4. -3. ] | [1 1 0] | 4.5 | [ 0.5 4. -3. ] | [ 0.5 4.5 5.5 -2.5 -1.5] | True |
| 13 | [ 0.5 4. -3. ] | [1 2 1] | 5.5 | [ 0.5 4. -3. ] | [ 0.5 4.5 5.5 -2.5 -1.5] | True |
| 14 | [ 0.5 4. -3. ] | [1 0 1] | -2.5 | [ 0.5 4. -3. ] | [ 0.5 4.5 5.5 -2.5 -1.5] | True |
| 15 | [ 0.5 4. -3. ] | [1 1 2] | -1.5 | [ 0.5 4. -3. ] | [ 0.5 4.5 5.5 -2.5 -1.5] | True |
+-----------+------------------+---------+------+------------------+----------------------------+-------------+
Batch Perceptron Learning Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# Batch Perceptron Learning Algorithm
import numpy as np
from prettytable import PrettyTable
# configuration variables
# -----------------------------------------------------------
# initial values
# a = [b, w1, w2]
a = [-25,6,3]
# learning rate
n = 1
epoch = 3
# dataset
# -----------------------------------------------------------
X = [[1,5],[2,5],[4,1],[5,1]]
Y = [1,1,-1,-1]
# Sequential Perceptron Learning Algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
update = 0
for i in range(len(Y)):
a_prev = a
# y = [1, x1, x2]
y = np.hstack((1,X[i]))
# calculate ay like wx+b = b + w1x1 + w2x2
ay = np.dot(a, y)
#update part ηω'yk
if ay * Y[i] <= 0:
if ay > 0:
update = update + n * y * (-1)
if ay <= 0:
update = update + n * y
cur_result = []
# evaluate
for index in range(len(Y)):
cur_result.append((np.dot(np.hstack((1,X[index])),a)))
# check if converage
is_converage = True
for index in range(len(Y)):
if cur_result[index] * Y[index] <= 0:
is_converage = False
# append result
result.append((str(i + 1 + (len(Y) * o)), np.round(a_prev, 4), np.round(y, 4), np.round(ay, 4), np.round(a, 4),np.round(cur_result, 4),is_converage))
# add update part to a
a = np.add(a, update)
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration', 'a', 'y', 'ay', 'a_new','over all result','is converage'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
+-----------+---------------+---------+-----+---------------+-------------------+--------------+
| iteration | a | y | ay | a_new | over all result | is converage |
+-----------+---------------+---------+-----+---------------+-------------------+--------------+
| 1 | [-25 6 3] | [1 1 5] | -4 | [-25 6 3] | [-4 2 2 8] | False |
| 2 | [-25 6 3] | [1 2 5] | 2 | [-25 6 3] | [-4 2 2 8] | False |
| 3 | [-25 6 3] | [1 4 1] | 2 | [-25 6 3] | [-4 2 2 8] | False |
| 4 | [-25 6 3] | [1 5 1] | 8 | [-25 6 3] | [-4 2 2 8] | False |
| 5 | [-26 -2 6] | [1 1 5] | 2 | [-26 -2 6] | [ 2 0 -28 -30] | False |
| 6 | [-26 -2 6] | [1 2 5] | 0 | [-26 -2 6] | [ 2 0 -28 -30] | False |
| 7 | [-26 -2 6] | [1 4 1] | -28 | [-26 -2 6] | [ 2 0 -28 -30] | False |
| 8 | [-26 -2 6] | [1 5 1] | -30 | [-26 -2 6] | [ 2 0 -28 -30] | False |
| 9 | [-25 0 11] | [1 1 5] | 30 | [-25 0 11] | [ 30 30 -14 -14] | True |
| 10 | [-25 0 11] | [1 2 5] | 30 | [-25 0 11] | [ 30 30 -14 -14] | True |
| 11 | [-25 0 11] | [1 4 1] | -14 | [-25 0 11] | [ 30 30 -14 -14] | True |
| 12 | [-25 0 11] | [1 5 1] | -14 | [-25 0 11] | [ 30 30 -14 -14] | True |
+-----------+---------------+---------+-----+---------------+-------------------+--------------+
Sequential Multiclass Perceptron Learning algorithm Python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# Sequential Multiclass Perceptron Learning algorithm
import numpy as np
from prettytable import PrettyTable
# configuration variables
# -----------------------------------------------------------
# initial values
# a = [b, w1, w2]
a = [[-0.5,0,-0.5],[-3,0.5,0],[0.5,1.5,-0.5]]
# learning rate
n = 1
epoch = 5
# dataset
# -----------------------------------------------------------
X = [[0,1],[1,0],[0.5,1.5],[1,1],[-0.5,0]]
Y = [1,1,2,2,3]
# Sequential Perceptron Learning Algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
for i in range(len(Y)):
a_prev = a.copy()
# y = [1, x1, x2]
y = np.hstack((1,X[i]))
# calculate ay like wx+b = b + w1x1 + w2x2
ay = np.dot(a, np.transpose([y]))
if all(x == ay[0] for x in ay):
j = 2
else:
j = np.argmax(ay)
true_y = Y[i] - 1
if j != true_y:
update = n * y
a[true_y] = np.add(a[true_y], update)
update = n * y * (-1)
a[j] = np.add(a[j], update)
cur_result = []
# evaluate
for index in range(len(Y)):
cur_result.append((np.dot(np.hstack((1,X[index])),np.transpose(a))))
# check if converage
is_converage = False
if np.array_equal(np.array(Y),np.argmax(cur_result,axis=1) + 1):
is_converage = True
# append result
result.append((str(i + 1 + (len(Y) * o)), np.round(a_prev, 4), np.round(y, 4), np.round(ay, 4),j+1, np.round(a, 4),np.round(cur_result, 4),np.argmax(cur_result,axis=1) + 1,is_converage))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration', 'a', 'y', 'ay','class', 'a_new','over all result','class result','is converage'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
+-----------+--------------------+------------------+-----------+-------+--------------------+-----------------------+--------------+--------------+
| iteration | a | y | ay | class | a_new | over all result | class result | is converage |
+-----------+--------------------+------------------+-----------+-------+--------------------+-----------------------+--------------+--------------+
| 1 | [[-0.5 0. -0.5] | [1 0 1] | [[-1.] | 3 | [[ 0.5 0. 0.5] | [[ 1. -3. -2. ] | [1 3 1 1 1] | False |
| | [-3. 0.5 0. ] | | [-3.] | | [-3. 0.5 0. ] | [ 0.5 -2.5 1. ] | | |
| | [ 0.5 1.5 -0.5]] | | [ 0.]] | | [-0.5 1.5 -1.5]] | [ 1.25 -2.75 -2. ] | | |
| | | | | | | [ 1. -2.5 -0.5 ] | | |
| | | | | | | [ 0.5 -3.25 -1.25]] | | |
| 2 | [[ 0.5 0. 0.5] | [1 1 0] | [[ 0.5] | 3 | [[ 1.5 1. 0.5] | [[ 2. -3. -3. ] | [1 1 1 1 1] | False |
| | [-3. 0.5 0. ] | | [-2.5] | | [-3. 0.5 0. ] | [ 2.5 -2.5 -1. ] | | |
| | [-0.5 1.5 -1.5]] | | [ 1. ]] | | [-1.5 0.5 -1.5]] | [ 2.75 -2.75 -3.5 ] | | |
| | | | | | | [ 3. -2.5 -2.5 ] | | |
| | | | | | | [ 1. -3.25 -1.75]] | | |
| 3 | [[ 1.5 1. 0.5] | [1. 0.5 1.5] | [[ 2.75] | 1 | [[ 0.5 0.5 -1. ] | [[-0.5 -0.5 -3. ] | [1 1 2 2 1] | False |
| | [-3. 0.5 0. ] | | [-2.75] | | [-2. 1. 1.5] | [ 1. -1. -1. ] | | |
| | [-1.5 0.5 -1.5]] | | [-3.5 ]] | | [-1.5 0.5 -1.5]] | [-0.75 0.75 -3.5 ] | | |
| | | | | | | [ 0. 0.5 -2.5 ] | | |
| | | | | | | [ 0.25 -2.5 -1.75]] | | |
| 4 | [[ 0.5 0.5 -1. ] | [1 1 1] | [[ 0. ] | 2 | [[ 0.5 0.5 -1. ] | [[-0.5 -0.5 -3. ] | [1 1 2 2 1] | False |
| | [-2. 1. 1.5] | | [ 0.5] | | [-2. 1. 1.5] | [ 1. -1. -1. ] | | |
| | [-1.5 0.5 -1.5]] | | [-2.5]] | | [-1.5 0.5 -1.5]] | [-0.75 0.75 -3.5 ] | | |
| | | | | | | [ 0. 0.5 -2.5 ] | | |
| | | | | | | [ 0.25 -2.5 -1.75]] | | |
| 5 | [[ 0.5 0.5 -1. ] | [ 1. -0.5 0. ] | [[ 0.25] | 1 | [[-0.5 1. -1. ] | [[-1.5 -0.5 -2. ] | [2 1 2 2 3] | False |
| | [-2. 1. 1.5] | | [-2.5 ] | | [-2. 1. 1.5] | [ 0.5 -1. -0.5 ] | | |
| | [-1.5 0.5 -1.5]] | | [-1.75]] | | [-0.5 0. -1.5]] | [-1.5 0.75 -2.75] | | |
| | | | | | | [-0.5 0.5 -2. ] | | |
| | | | | | | [-1. -2.5 -0.5 ]] | | |
| 6 | [[-0.5 1. -1. ] | [1 0 1] | [[-1.5] | 2 | [[ 0.5 1. 0. ] | [[ 0.5 -2.5 -2. ] | [1 1 1 1 1] | False |
| | [-2. 1. 1.5] | | [-0.5] | | [-3. 1. 0.5] | [ 1.5 -2. -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-2. ]] | | [-0.5 0. -1.5]] | [ 1. -1.75 -2.75] | | |
| | | | | | | [ 1.5 -1.5 -2. ] | | |
| | | | | | | [ 0. -3.5 -0.5 ]] | | |
| 7 | [[ 0.5 1. 0. ] | [1 1 0] | [[ 1.5] | 1 | [[ 0.5 1. 0. ] | [[ 0.5 -2.5 -2. ] | [1 1 1 1 1] | False |
| | [-3. 1. 0.5] | | [-2. ] | | [-3. 1. 0.5] | [ 1.5 -2. -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-0.5]] | | [-0.5 0. -1.5]] | [ 1. -1.75 -2.75] | | |
| | | | | | | [ 1.5 -1.5 -2. ] | | |
| | | | | | | [ 0. -3.5 -0.5 ]] | | |
| 8 | [[ 0.5 1. 0. ] | [1. 0.5 1.5] | [[ 1. ] | 1 | [[-0.5 0.5 -1.5] | [[-2. 0. -2. ] | [2 1 2 2 3] | False |
| | [-3. 1. 0.5] | | [-1.75] | | [-2. 1.5 2. ] | [ 0. -0.5 -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-2.75]] | | [-0.5 0. -1.5]] | [-2.5 1.75 -2.75] | | |
| | | | | | | [-1.5 1.5 -2. ] | | |
| | | | | | | [-0.75 -2.75 -0.5 ]] | | |
| 9 | [[-0.5 0.5 -1.5] | [1 1 1] | [[-1.5] | 2 | [[-0.5 0.5 -1.5] | [[-2. 0. -2. ] | [2 1 2 2 3] | False |
| | [-2. 1.5 2. ] | | [ 1.5] | | [-2. 1.5 2. ] | [ 0. -0.5 -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-2. ]] | | [-0.5 0. -1.5]] | [-2.5 1.75 -2.75] | | |
| | | | | | | [-1.5 1.5 -2. ] | | |
| | | | | | | [-0.75 -2.75 -0.5 ]] | | |
| 10 | [[-0.5 0.5 -1.5] | [ 1. -0.5 0. ] | [[-0.75] | 3 | [[-0.5 0.5 -1.5] | [[-2. 0. -2. ] | [2 1 2 2 3] | False |
| | [-2. 1.5 2. ] | | [-2.75] | | [-2. 1.5 2. ] | [ 0. -0.5 -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-0.5 ]] | | [-0.5 0. -1.5]] | [-2.5 1.75 -2.75] | | |
| | | | | | | [-1.5 1.5 -2. ] | | |
| | | | | | | [-0.75 -2.75 -0.5 ]] | | |
| 11 | [[-0.5 0.5 -1.5] | [1 0 1] | [[-2.] | 2 | [[ 0.5 0.5 -0.5] | [[ 0. -2. -2. ] | [1 1 1 1 1] | False |
| | [-2. 1.5 2. ] | | [ 0.] | | [-3. 1.5 1. ] | [ 1. -1.5 -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-2.]] | | [-0.5 0. -1.5]] | [ 0. -0.75 -2.75] | | |
| | | | | | | [ 0.5 -0.5 -2. ] | | |
| | | | | | | [ 0.25 -3.75 -0.5 ]] | | |
| 12 | [[ 0.5 0.5 -0.5] | [1 1 0] | [[ 1. ] | 1 | [[ 0.5 0.5 -0.5] | [[ 0. -2. -2. ] | [1 1 1 1 1] | False |
| | [-3. 1.5 1. ] | | [-1.5] | | [-3. 1.5 1. ] | [ 1. -1.5 -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-0.5]] | | [-0.5 0. -1.5]] | [ 0. -0.75 -2.75] | | |
| | | | | | | [ 0.5 -0.5 -2. ] | | |
| | | | | | | [ 0.25 -3.75 -0.5 ]] | | |
| 13 | [[ 0.5 0.5 -0.5] | [1. 0.5 1.5] | [[ 0. ] | 1 | [[-0.5 0. -2. ] | [[-2.5 0.5 -2. ] | [2 2 2 2 1] | False |
| | [-3. 1.5 1. ] | | [-0.75] | | [-2. 2. 2.5] | [-0.5 0. -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-2.75]] | | [-0.5 0. -1.5]] | [-3.5 2.75 -2.75] | | |
| | | | | | | [-2.5 2.5 -2. ] | | |
| | | | | | | [-0.5 -3. -0.5 ]] | | |
| 14 | [[-0.5 0. -2. ] | [1 1 1] | [[-2.5] | 2 | [[-0.5 0. -2. ] | [[-2.5 0.5 -2. ] | [2 2 2 2 1] | False |
| | [-2. 2. 2.5] | | [ 2.5] | | [-2. 2. 2.5] | [-0.5 0. -0.5 ] | | |
| | [-0.5 0. -1.5]] | | [-2. ]] | | [-0.5 0. -1.5]] | [-3.5 2.75 -2.75] | | |
| | | | | | | [-2.5 2.5 -2. ] | | |
| | | | | | | [-0.5 -3. -0.5 ]] | | |
| 15 | [[-0.5 0. -2. ] | [ 1. -0.5 0. ] | [[-0.5] | 1 | [[-1.5 0.5 -2. ] | [[-3.5 0.5 -1. ] | [2 2 2 2 3] | False |
| | [-2. 2. 2.5] | | [-3. ] | | [-2. 2. 2.5] | [-1. 0. 0. ] | | |
| | [-0.5 0. -1.5]] | | [-0.5]] | | [ 0.5 -0.5 -1.5]] | [-4.25 2.75 -2. ] | | |
| | | | | | | [-3. 2.5 -1.5 ] | | |
| | | | | | | [-1.75 -3. 0.75]] | | |
| 16 | [[-1.5 0.5 -2. ] | [1 0 1] | [[-3.5] | 2 | [[-0.5 0.5 -1. ] | [[-1.5 -1.5 -1. ] | [3 1 2 2 3] | False |
| | [-2. 2. 2.5] | | [ 0.5] | | [-3. 2. 1.5] | [ 0. -1. 0. ] | | |
| | [ 0.5 -0.5 -1.5]] | | [-1. ]] | | [ 0.5 -0.5 -1.5]] | [-1.75 0.25 -2. ] | | |
| | | | | | | [-1. 0.5 -1.5 ] | | |
| | | | | | | [-0.75 -4. 0.75]] | | |
| 17 | [[-0.5 0.5 -1. ] | [1 1 0] | [[ 0.] | 1 | [[-0.5 0.5 -1. ] | [[-1.5 -1.5 -1. ] | [3 1 2 2 3] | False |
| | [-3. 2. 1.5] | | [-1.] | | [-3. 2. 1.5] | [ 0. -1. 0. ] | | |
| | [ 0.5 -0.5 -1.5]] | | [ 0.]] | | [ 0.5 -0.5 -1.5]] | [-1.75 0.25 -2. ] | | |
| | | | | | | [-1. 0.5 -1.5 ] | | |
| | | | | | | [-0.75 -4. 0.75]] | | |
| 18 | [[-0.5 0.5 -1. ] | [1. 0.5 1.5] | [[-1.75] | 2 | [[-0.5 0.5 -1. ] | [[-1.5 -1.5 -1. ] | [3 1 2 2 3] | False |
| | [-3. 2. 1.5] | | [ 0.25] | | [-3. 2. 1.5] | [ 0. -1. 0. ] | | |
| | [ 0.5 -0.5 -1.5]] | | [-2. ]] | | [ 0.5 -0.5 -1.5]] | [-1.75 0.25 -2. ] | | |
| | | | | | | [-1. 0.5 -1.5 ] | | |
| | | | | | | [-0.75 -4. 0.75]] | | |
| 19 | [[-0.5 0.5 -1. ] | [1 1 1] | [[-1. ] | 2 | [[-0.5 0.5 -1. ] | [[-1.5 -1.5 -1. ] | [3 1 2 2 3] | False |
| | [-3. 2. 1.5] | | [ 0.5] | | [-3. 2. 1.5] | [ 0. -1. 0. ] | | |
| | [ 0.5 -0.5 -1.5]] | | [-1.5]] | | [ 0.5 -0.5 -1.5]] | [-1.75 0.25 -2. ] | | |
| | | | | | | [-1. 0.5 -1.5 ] | | |
| | | | | | | [-0.75 -4. 0.75]] | | |
| 20 | [[-0.5 0.5 -1. ] | [ 1. -0.5 0. ] | [[-0.75] | 3 | [[-0.5 0.5 -1. ] | [[-1.5 -1.5 -1. ] | [3 1 2 2 3] | False |
| | [-3. 2. 1.5] | | [-4. ] | | [-3. 2. 1.5] | [ 0. -1. 0. ] | | |
| | [ 0.5 -0.5 -1.5]] | | [ 0.75]] | | [ 0.5 -0.5 -1.5]] | [-1.75 0.25 -2. ] | | |
| | | | | | | [-1. 0.5 -1.5 ] | | |
| | | | | | | [-0.75 -4. 0.75]] | | |
| 21 | [[-0.5 0.5 -1. ] | [1 0 1] | [[-1.5] | 3 | [[ 0.5 0.5 0. ] | [[ 0.5 -1.5 -3. ] | [1 1 1 1 1] | False |
| | [-3. 2. 1.5] | | [-1.5] | | [-3. 2. 1.5] | [ 1. -1. -1. ] | | |
| | [ 0.5 -0.5 -1.5]] | | [-1. ]] | | [-0.5 -0.5 -2.5]] | [ 0.75 0.25 -4.5 ] | | |
| | | | | | | [ 1. 0.5 -3.5 ] | | |
| | | | | | | [ 0.25 -4. -0.25]] | | |
| 22 | [[ 0.5 0.5 0. ] | [1 1 0] | [[ 1.] | 1 | [[ 0.5 0.5 0. ] | [[ 0.5 -1.5 -3. ] | [1 1 1 1 1] | False |
| | [-3. 2. 1.5] | | [-1.] | | [-3. 2. 1.5] | [ 1. -1. -1. ] | | |
| | [-0.5 -0.5 -2.5]] | | [-1.]] | | [-0.5 -0.5 -2.5]] | [ 0.75 0.25 -4.5 ] | | |
| | | | | | | [ 1. 0.5 -3.5 ] | | |
| | | | | | | [ 0.25 -4. -0.25]] | | |
| 23 | [[ 0.5 0.5 0. ] | [1. 0.5 1.5] | [[ 0.75] | 1 | [[-0.5 0. -1.5] | [[-2. 1. -3. ] | [2 2 2 2 3] | False |
| | [-3. 2. 1.5] | | [ 0.25] | | [-2. 2.5 3. ] | [-0.5 0.5 -1. ] | | |
| | [-0.5 -0.5 -2.5]] | | [-4.5 ]] | | [-0.5 -0.5 -2.5]] | [-2.75 3.75 -4.5 ] | | |
| | | | | | | [-2. 3.5 -3.5 ] | | |
| | | | | | | [-0.5 -3.25 -0.25]] | | |
| 24 | [[-0.5 0. -1.5] | [1 1 1] | [[-2. ] | 2 | [[-0.5 0. -1.5] | [[-2. 1. -3. ] | [2 2 2 2 3] | False |
| | [-2. 2.5 3. ] | | [ 3.5] | | [-2. 2.5 3. ] | [-0.5 0.5 -1. ] | | |
| | [-0.5 -0.5 -2.5]] | | [-3.5]] | | [-0.5 -0.5 -2.5]] | [-2.75 3.75 -4.5 ] | | |
| | | | | | | [-2. 3.5 -3.5 ] | | |
| | | | | | | [-0.5 -3.25 -0.25]] | | |
| 25 | [[-0.5 0. -1.5] | [ 1. -0.5 0. ] | [[-0.5 ] | 3 | [[-0.5 0. -1.5] | [[-2. 1. -3. ] | [2 2 2 2 3] | False |
| | [-2. 2.5 3. ] | | [-3.25] | | [-2. 2.5 3. ] | [-0.5 0.5 -1. ] | | |
| | [-0.5 -0.5 -2.5]] | | [-0.25]] | | [-0.5 -0.5 -2.5]] | [-2.75 3.75 -4.5 ] | | |
| | | | | | | [-2. 3.5 -3.5 ] | | |
| | | | | | | [-0.5 -3.25 -0.25]] | | |
+-----------+--------------------+------------------+-----------+-------+--------------------+-----------------------+--------------+--------------+
Minimum Squared Error (MSE) Procedures



Minimum Squared Error (MSE) Procedures Python code
1
2
3
4
5
6
# Typically Y is rectangular, so the solution is given by: a=Y† b
b = np.dot(y, a)
# Cost function
# e2= ∥ Ya−b ∥^2, J s (a)= 1/2‖ Ya−b ‖^2
e = (np.dot(y, a)-b)(np.dot(y, a)-b)
Widrow-Hoff (or LMS) Learning Algorithm


Sequential Widrow-Hoff Learning Algorithm Python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# Sequential Widrow-Hoff Learning Algorithm
import numpy as np
from prettytable import PrettyTable
# configuration variables
# -----------------------------------------------------------
# initial values
a = [-1.5,5,-1]
# learning rate
n = 0.2
# iterations
# iterations = 150
epoch = 2
# dataset
# -----------------------------------------------------------
X = [[0,0],[1,0],[2,1],[0,1],[1,2]]
Y = [1,1,1,-1,-1]
# margin vector
b = np.ones(len(X))*2
# sequential widrow-hoff learning algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
for i in range(len(Y)):
a_prev = a
if Y[i] == 1:
y = np.hstack((Y[i],X[i]))
else:
y = np.hstack((Y[i],np.array(X[i])*(-1)))
# calculate ay
ay = np.dot(a, y)
# calculate update part, η(b−ay)*y
update = n * (b[i] - ay) * y
# add update part to a
a = np.add(a, update)
cur_result = []
# evaluate
for index in range(len(Y)):
y = np.hstack((1,X[index]))
cur_result.append(np.dot(a, y))
# check if converage
is_converage = True
for index in range(len(Y)):
if cur_result[index] * Y[index] < 0:
is_converage = False
# append result
result.append((str(i + 1 + (len(Y) * o)), np.round(a_prev, 4), np.round(y, 4), np.round(ay, 4), np.round(a, 4),np.round(cur_result, 4),is_converage))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration', 'a', 'y', 'ay', 'a_new','over all result','is converage'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
+-----------+---------------------------+---------+---------+---------------------------+-------------------------------------------+-------------+
| iteration | a | y | ay | a_new | over all result | is converge |
+-----------+---------------------------+---------+---------+---------------------------+-------------------------------------------+-------------+
| 1 | [-1.5 5. -1. ] | [1 1 2] | -1.5 | [-0.8 5. -1. ] | [-0.8 4.2 8.2 -1.8 2.2] | False |
| 2 | [-0.8 5. -1. ] | [1 1 2] | 4.2 | [-1.24 4.56 -1. ] | [-1.24 3.32 6.88 -2.24 1.32] | False |
| 3 | [-1.24 4.56 -1. ] | [1 1 2] | 6.88 | [-2.216 2.608 -1.976] | [-2.216 0.392 1.024 -4.192 -3.56 ] | False |
| 4 | [-2.216 2.608 -1.976] | [1 1 2] | 4.192 | [-1.7776 2.608 -1.5376] | [-1.7776 0.8304 1.9008 -3.3152 -2.2448] | False |
| 5 | [-1.7776 2.608 -1.5376] | [1 1 2] | 2.2448 | [-1.7286 2.657 -1.4397] | [-1.7286 0.9283 2.1456 -3.1683 -1.951 ] | False |
| 6 | [-1.7286 2.657 -1.4397] | [1 1 2] | -1.7286 | [-0.9829 2.657 -1.4397] | [-0.9829 1.674 2.8913 -2.4226 -1.2053] | False |
| 7 | [-0.9829 2.657 -1.4397] | [1 1 2] | 1.674 | [-0.9177 2.7222 -1.4397] | [-0.9177 1.8044 3.0869 -2.3574 -1.0749] | False |
| 8 | [-0.9177 2.7222 -1.4397] | [1 1 2] | 3.0869 | [-1.1351 2.2874 -1.6571] | [-1.1351 1.1523 1.7826 -2.7922 -2.1618] | False |
| 9 | [-1.1351 2.2874 -1.6571] | [1 1 2] | 2.7922 | [-0.9767 2.2874 -1.4986] | [-0.9767 1.3107 2.0995 -2.4753 -1.6865] | False |
| 10 | [-0.9767 2.2874 -1.4986] | [1 1 2] | 1.6865 | [-1.0394 2.2247 -1.624 ] | [-1.0394 1.1853 1.786 -2.6634 -2.0627] | False |
+-----------+---------------------------+---------+---------+---------------------------+-------------------------------------------+-------------+
Comments powered by Disqus.