Deep Learning: Feature Extraction
Here is my Deep Learning Full Tutorial!
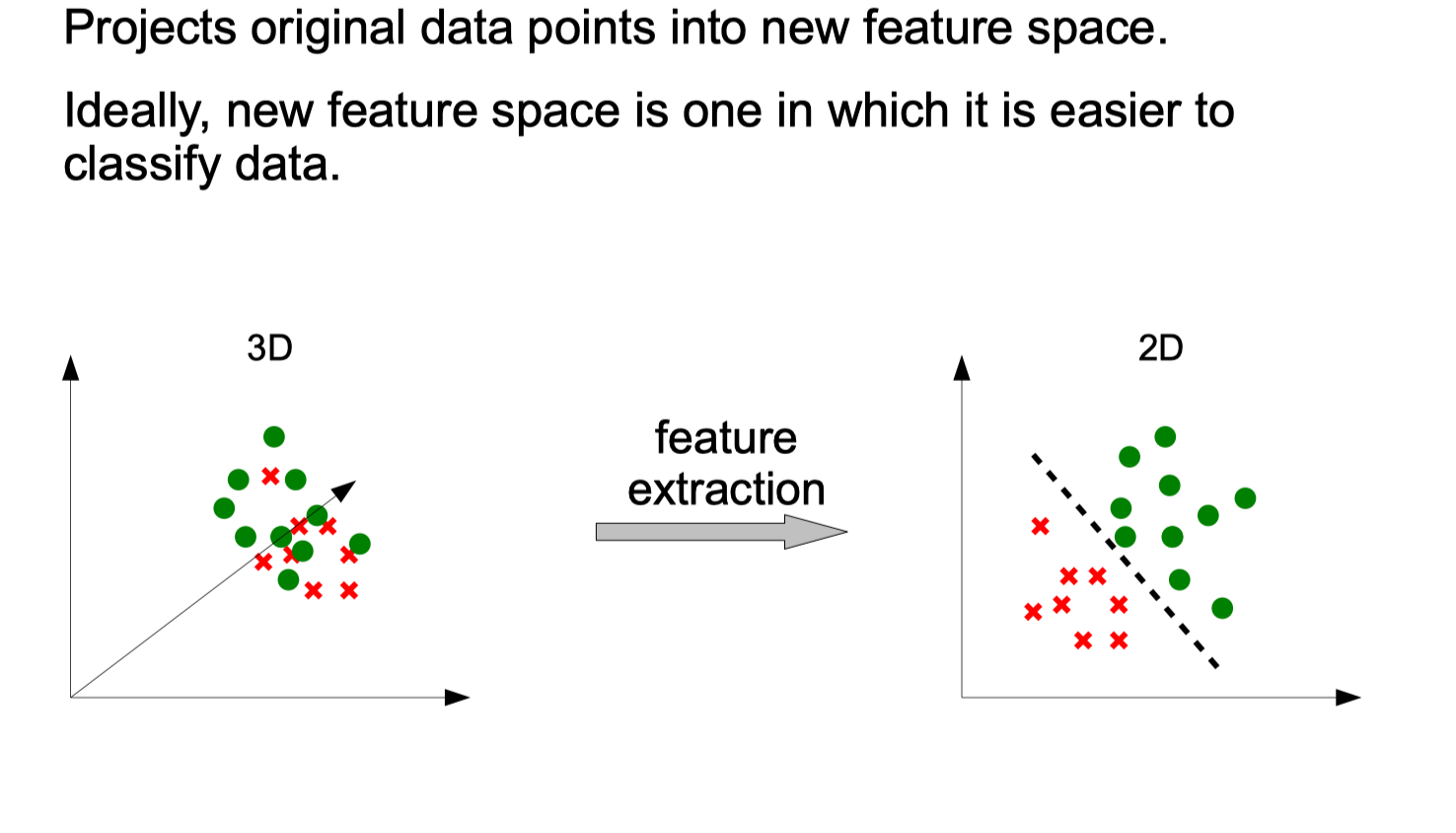
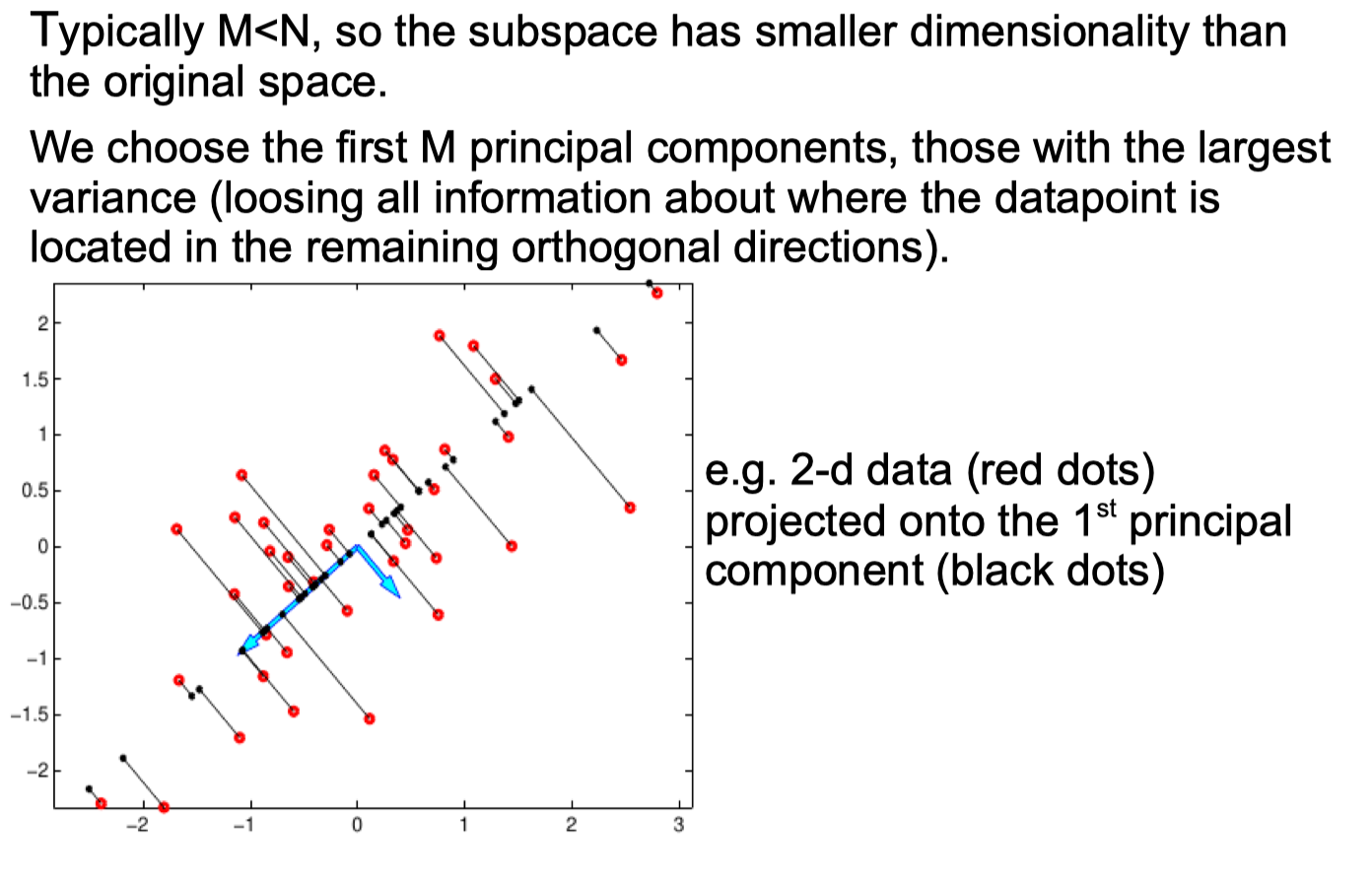
Principal Components Analysis


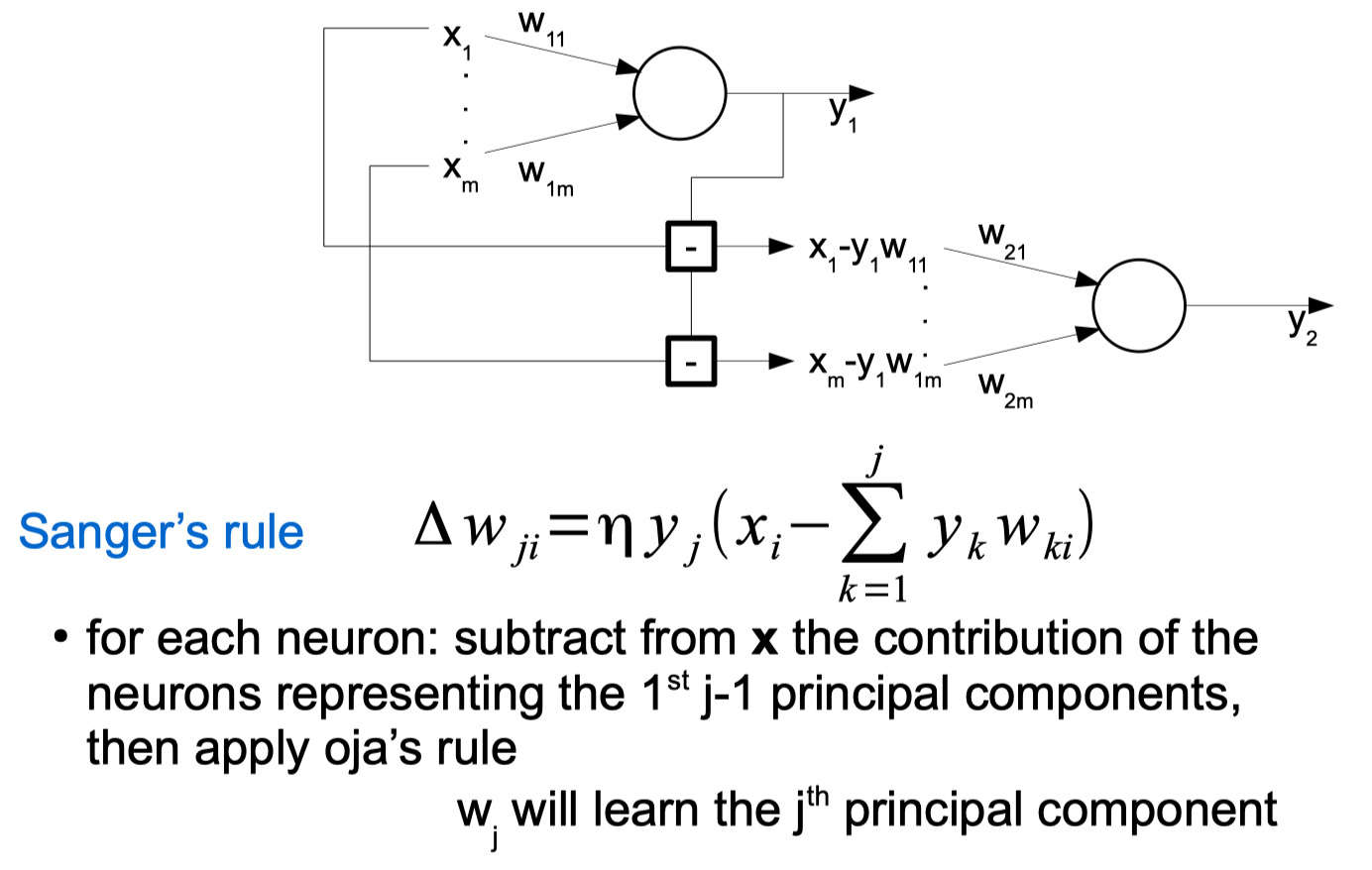
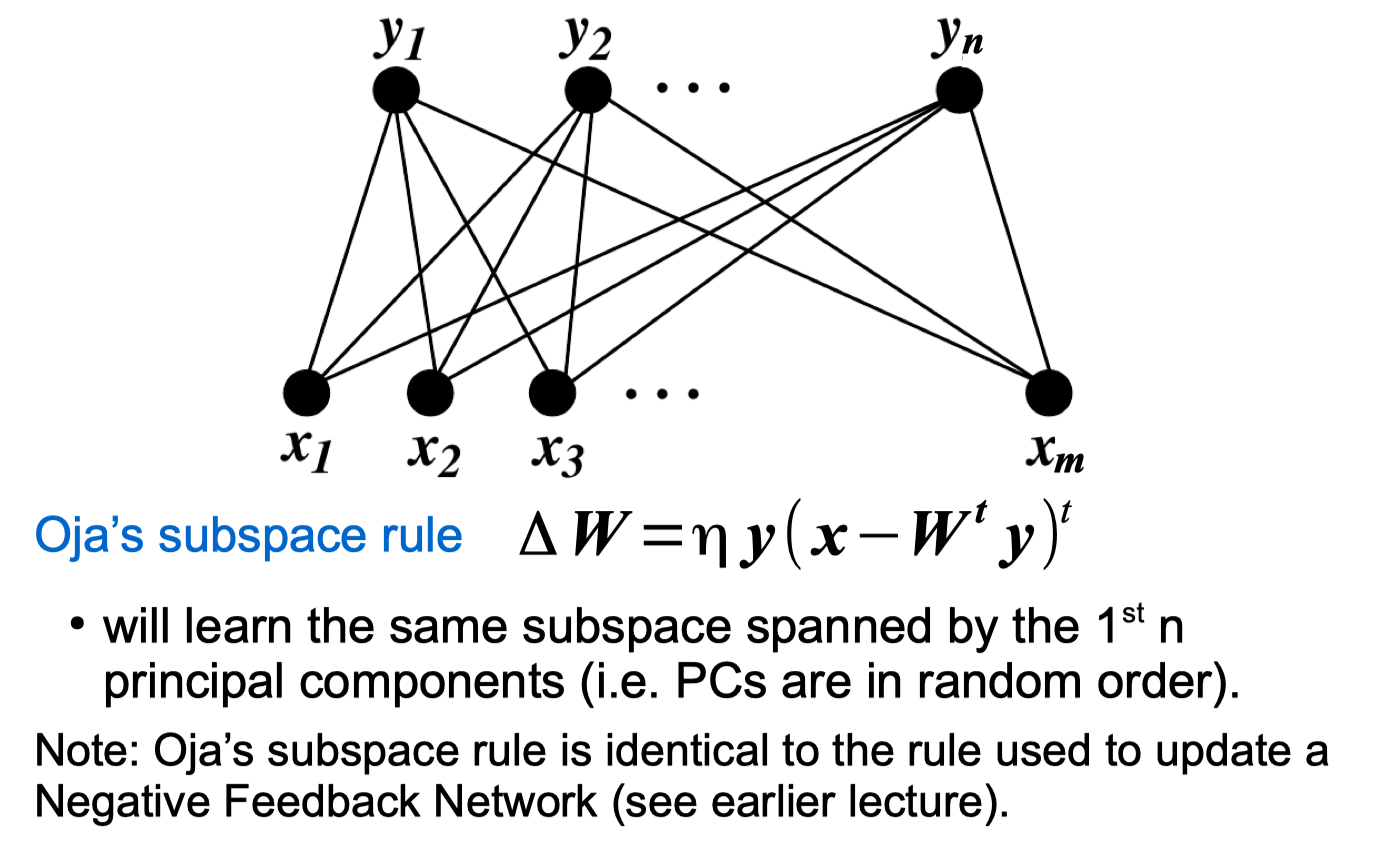
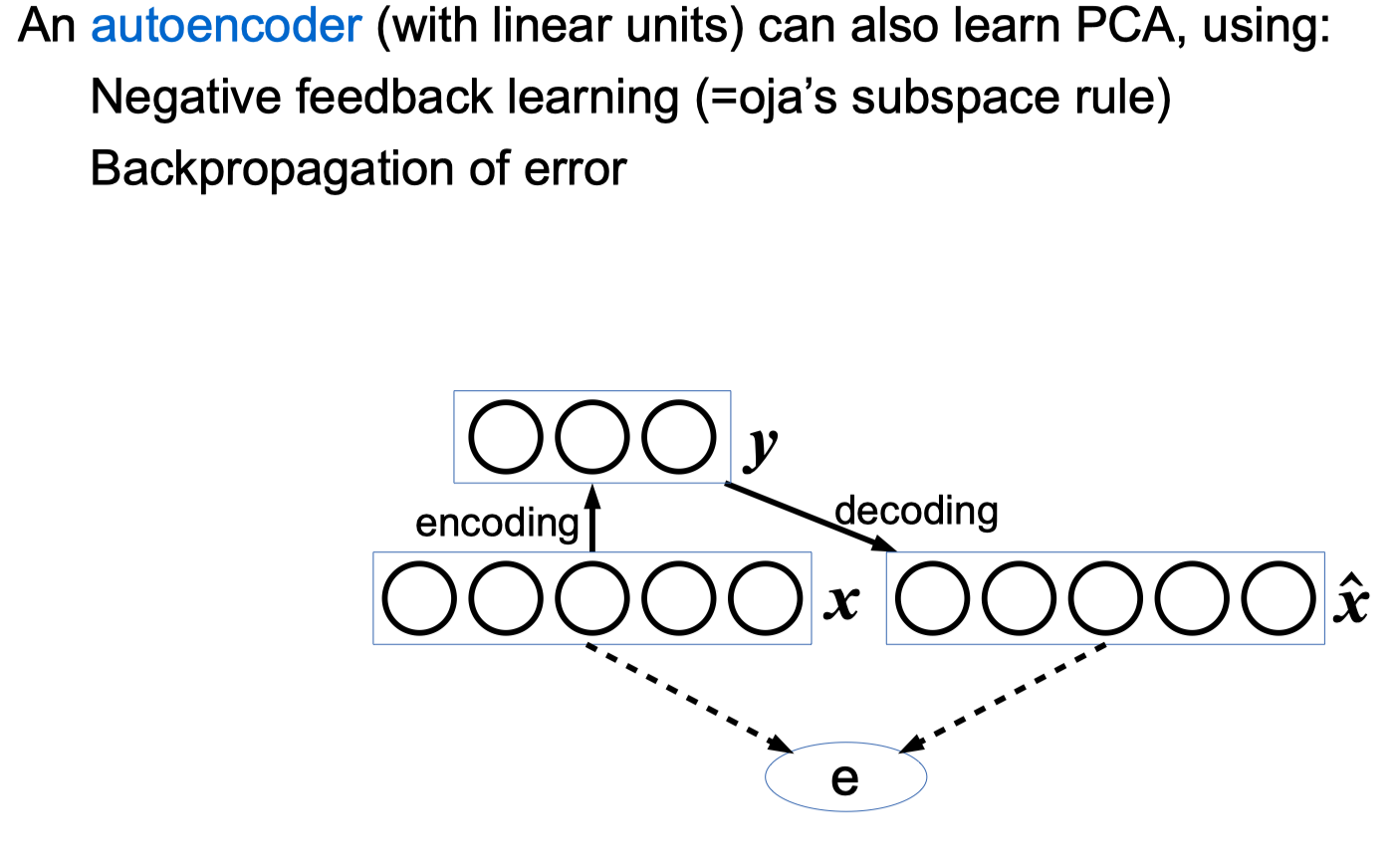
Traditional PCA python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
def pca(dataset, dim):
X = dataset
print(X.mean(axis=1, keepdims=True))
Y = X - X.mean(axis=1, keepdims=True)
print("X-mean = \n",Y)
C = []
for i in range(len(np.transpose(Y))):
C.append(np.dot(Y[:, [i]], np.transpose(Y[:, [i]])))
C = np.array(C)
C = np.sum(C, axis=0) / len(np.transpose(Y))
print("Conv = \n", C)
egv, egva = np.linalg.eigh(C)
print("egv = \n", egv)
print("egvalue = \n", egva)
vnew = []
for i in range(dim):
result = np.where(egv == np.partition(egv.flatten(), -(i + 1))[-(i + 1)])
vnew.append(egva[:, result[0][0]])
vnew = np.array(vnew)
print(vnew)
newsample = np.dot(vnew, Y)
return newsample
data = np.array([[4, 2, 2], [0, -2, 2], [2, 4, 2], [-2, 0, 2]])
data = np.transpose(data)
print("result = \n", pca(data, 2))
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
[[1.]
[1.]
[2.]]
X-mean =
[[ 3. -1. 1. -3.]
[ 1. -3. 3. -1.]
[ 0. 0. 0. 0.]]
Conv =
[[5. 3. 0.]
[3. 5. 0.]
[0. 0. 0.]]
egv =
[0. 2. 8.]
egvalue =
[[ 0. -0.70710678 0.70710678]
[ 0. 0.70710678 0.70710678]
[ 1. 0. 0. ]]
[[ 0.70710678 0.70710678 0. ]
[-0.70710678 0.70710678 0. ]]
result =
[[ 2.82842712 -2.82842712 2.82842712 -2.82842712]
[-1.41421356 -1.41421356 1.41421356 1.41421356]]
Neural Networks for PCA (Hebbian learning) python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
from prettytable import PrettyTable
# configuration variables
# -----------------------------------------------------------
# initial values
w = [0.5,-0.2]
# learning rate
n = 0.1
# iterations
# iterations = 150
epoch = 2
# dataset
# -----------------------------------------------------------
X = [[0,1],[1,2],[3,1],[-1,-2],[-3,-2]]
# Neural Networks for PCA algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
for i in range(len(X)):
w_prev = w
x = X[i]
y = np.dot(x,np.transpose(w))
# calculate update part, ηyx
update = (n*y) * np.array(x)
# add update part to w
w = np.add(w, update)
# append result
result.append((str(i + 1 + (len(X) * o)), np.round(w_prev, 4), np.round(x, 4), np.round(y, 4), np.round(update, 4),np.round(w, 4)))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration', 'w', 'x', 'y', 'ηyx','w_new'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
+-----------+-----------------+---------+----------+-----------------+-------------------+
| iteration | w | x | y | ηyx | w_new |
+-----------+-----------------+---------+----------+-----------------+-------------------+
| 1 | [ 0.5 -0.2] | [0 1] | -0.2 | [-0. -0.02] | [ 0.5 -0.22] |
| 2 | [ 0.5 -0.22] | [1 2] | 0.06 | [0.006 0.012] | [ 0.506 -0.208] |
| 3 | [ 0.506 -0.208] | [3 1] | 1.31 | [0.393 0.131] | [ 0.899 -0.077] |
| 4 | [ 0.899 -0.077] | [-1 -2] | -0.745 | [0.0745 0.149 ] | [0.9735 0.072 ] |
| 5 | [0.9735 0.072 ] | [-3 -2] | -3.0645 | [0.9194 0.6129] | [1.8928 0.6849] |
| 6 | [1.8928 0.6849] | [0 1] | 0.6849 | [0. 0.0685] | [1.8928 0.7534] |
| 7 | [1.8928 0.7534] | [1 2] | 3.3996 | [0.34 0.6799] | [2.2328 1.4333] |
| 8 | [2.2328 1.4333] | [3 1] | 8.1318 | [2.4395 0.8132] | [4.6723 2.2465] |
| 9 | [4.6723 2.2465] | [-1 -2] | -9.1653 | [0.9165 1.8331] | [5.5889 4.0796] |
| 10 | [5.5889 4.0796] | [-3 -2] | -24.9257 | [7.4777 4.9851] | [13.0666 9.0647] |
+-----------+-----------------+---------+----------+-----------------+-------------------+
Neural Networks for PCA (Oja’s rule)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
from prettytable import PrettyTable
# configuration variables
# -----------------------------------------------------------
# initial values
w = [0.5,-0.2]
# learning rate
n = 0.1
# iterations
# iterations = 150
epoch = 2
# dataset
# -----------------------------------------------------------
X = [[0,1],[1,2],[3,1],[-1,-2],[-3,-2]]
# Neural Networks for PCA algorithm
# -----------------------------------------------------------
result = []
for o in range(epoch):
for i in range(len(X)):
w_prev = w
x = X[i]
y = np.dot(x,np.transpose(w))
# calculate update part, ηyx
update = (n*y) * (np.array(x) - np.dot(y,w))
# add update part to w
w = np.add(w, update)
# append result
result.append((str(i + 1 + (len(X) * o)), np.round(w_prev, 4), np.round(x, 4), np.round(y, 4), np.round(update, 4),np.round(w, 4)))
# prettytable
# -----------------------------------------------------------
pt = PrettyTable(('iteration', 'w', 'x', 'y', 'ηyx','w_new'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
+-----------+-------------------+---------+---------+-------------------+-------------------+
| iteration | w | x | y | ηyx | w_new |
+-----------+-------------------+---------+---------+-------------------+-------------------+
| 1 | [ 0.5 -0.2] | [0 1] | -0.2 | [-0.002 -0.0192] | [ 0.498 -0.2192] |
| 2 | [ 0.498 -0.2192] | [1 2] | 0.0596 | [0.0058 0.012 ] | [ 0.5038 -0.2072] |
| 3 | [ 0.5038 -0.2072] | [3 1] | 1.3041 | [0.3056 0.1657] | [ 0.8093 -0.0415] |
| 4 | [ 0.8093 -0.0415] | [-1 -2] | -0.7263 | [0.0299 0.1474] | [0.8393 0.1059] |
| 5 | [0.8393 0.1059] | [-3 -2] | -2.7296 | [0.1936 0.467 ] | [1.0328 0.5729] |
| 6 | [1.0328 0.5729] | [0 1] | 0.5729 | [-0.0339 0.0385] | [0.9989 0.6114] |
| 7 | [0.9989 0.6114] | [1 2] | 2.2217 | [-0.2709 0.1425] | [0.728 0.754] |
| 8 | [0.728 0.754] | [3 1] | 2.938 | [ 0.253 -0.357] | [0.981 0.3969] |
| 9 | [0.981 0.3969] | [-1 -2] | -1.7749 | [-0.1316 0.2299] | [0.8495 0.6269] |
| 10 | [0.8495 0.6269] | [-3 -2] | -3.8021 | [-0.0873 -0.1458] | [0.7621 0.4811] |
+-----------+-------------------+---------+---------+-------------------+-------------------+
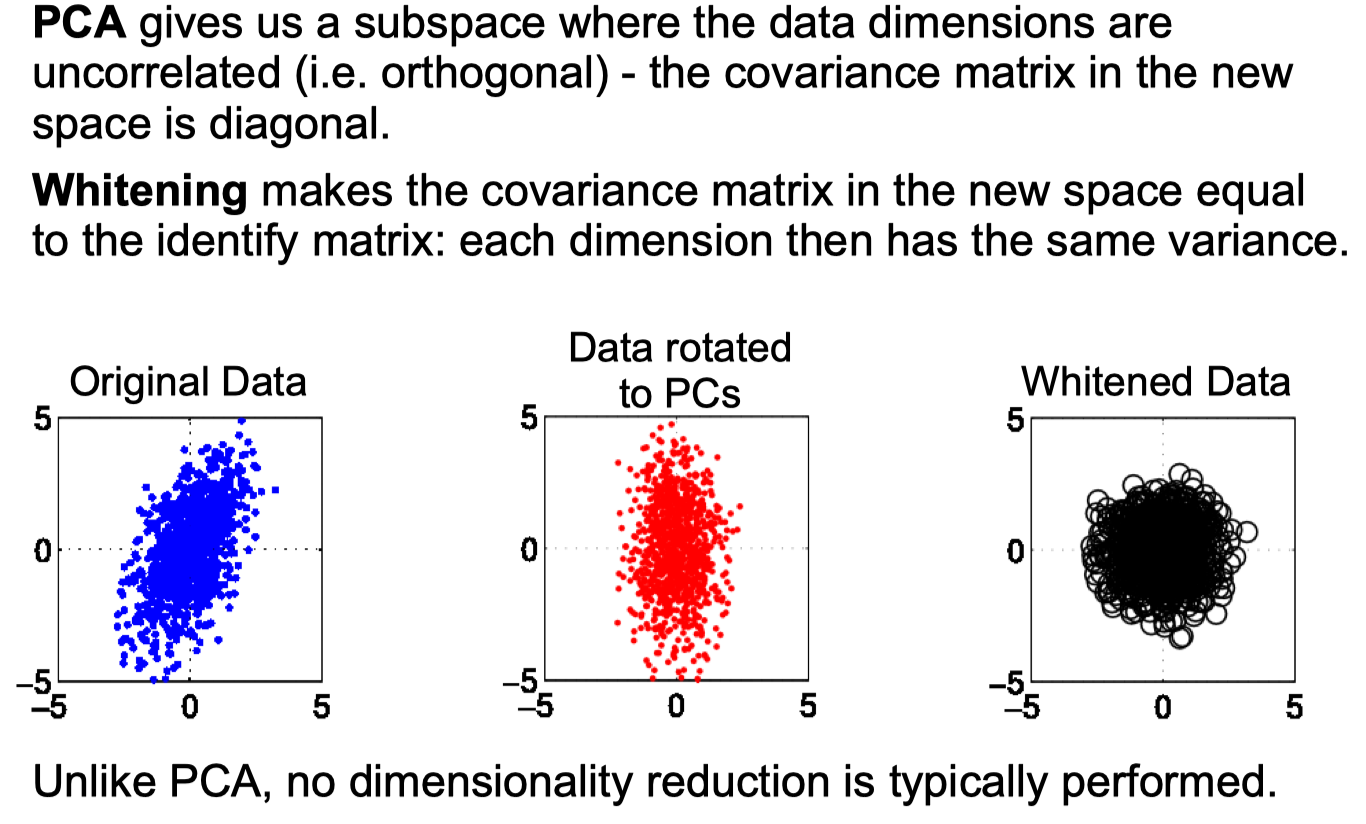
Whitening Transform
Linear Discriminant Analysis
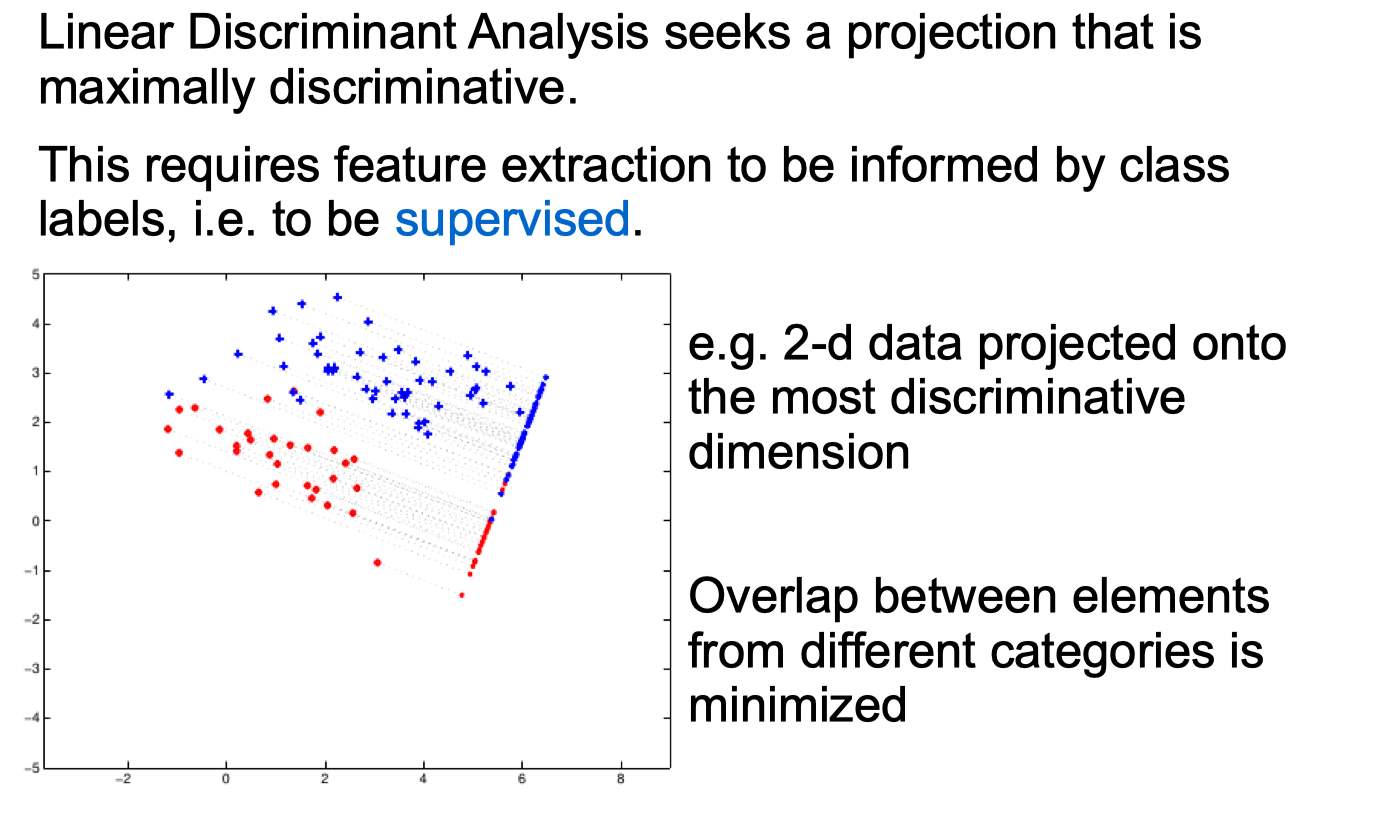
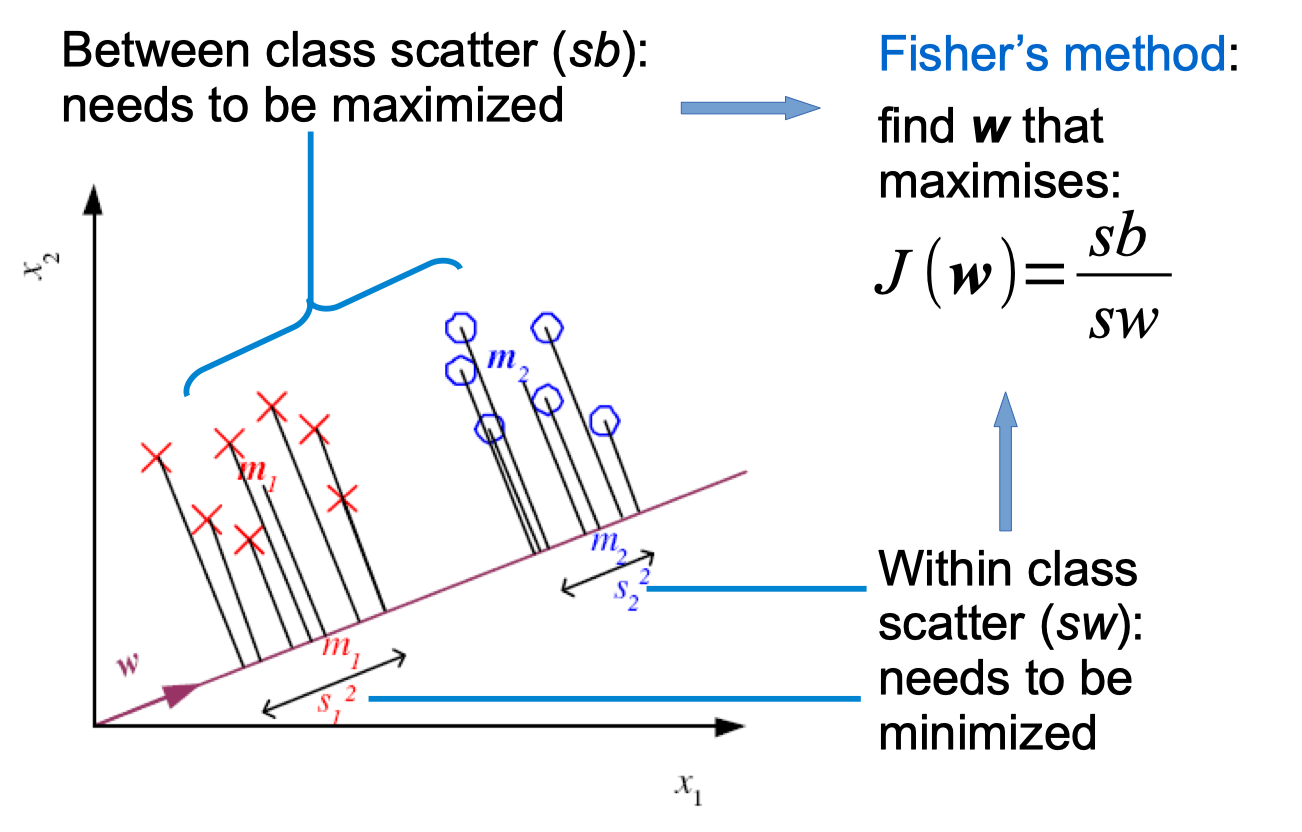
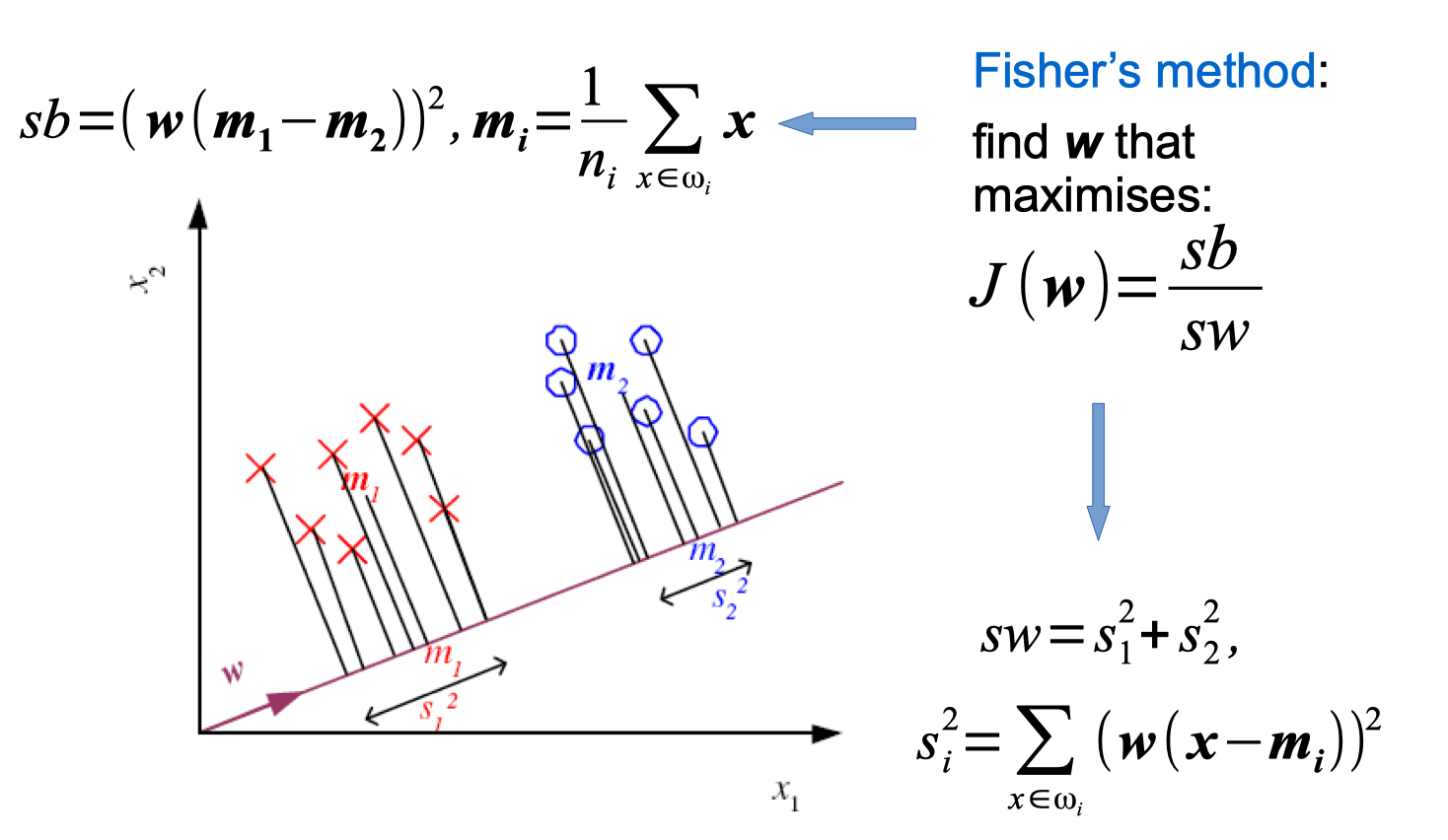
Linear Discriminant Analysis (LDA) python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
w1 = [-1,5]
w2 = [2,-3]
x1 = [
[1,2],
[2,1],
[3,3]]
x2 = [
[6,5],
[7,8]
]
result = []
def J(w,x1,x2):
sb = np.power(np.abs(np.dot(w,np.transpose(np.array(x1).mean(axis=0)-np.array(x2).mean(axis=0)))),2)
sw = sum(np.power(np.dot(w,np.transpose(x1 - np.array(x1).mean(axis=0))),2)) + sum(np.power(np.dot(w,np.transpose(x2 - np.array(x2).mean(axis=0))),2))
global result
result.append([w,np.array(x1).mean(axis=0),np.array(x2).mean(axis=0),np.array(x1).mean(axis=0)-np.array(x2).mean(axis=0),sb,sw,round(sb/sw,4)])
return sb/sw
J(w1,x1,x2)
J(w2,x1,x2)
pt = PrettyTable(('w','m1','m2','m1-m2','sb = |wT (m1 - m2)|^2','sw = (sum(wT(x-m1))^2 + sum(wT(x-m2))^2','J(w) = sb/sw'))
for row in result: pt.add_row(row)
print(pt)
Output
1
2
3
4
5
6
+---------+---------+-----------+-------------+------------------------+----------------------------------------+--------------+
| w | m1 | m2 | m1-m2 | sb = |wT (m1 - m2)|^2 | sw = (sum(wT(x-m1))2 + sum(wT(x-m2))^2 | J(w) = sb/sw |
+---------+---------+-----------+-------------+------------------------+----------------------------------------+--------------+
| [-1, 5] | [2. 2.] | [6.5 6.5] | [-4.5 -4.5] | 324.0 | 140.0 | 2.3143 |
| [2, -3] | [2. 2.] | [6.5 6.5] | [-4.5 -4.5] | 20.25 | 38.5 | 0.526 |
+---------+---------+-----------+-------------+------------------------+----------------------------------------+--------------+
Independent Component Analysis (ICA)



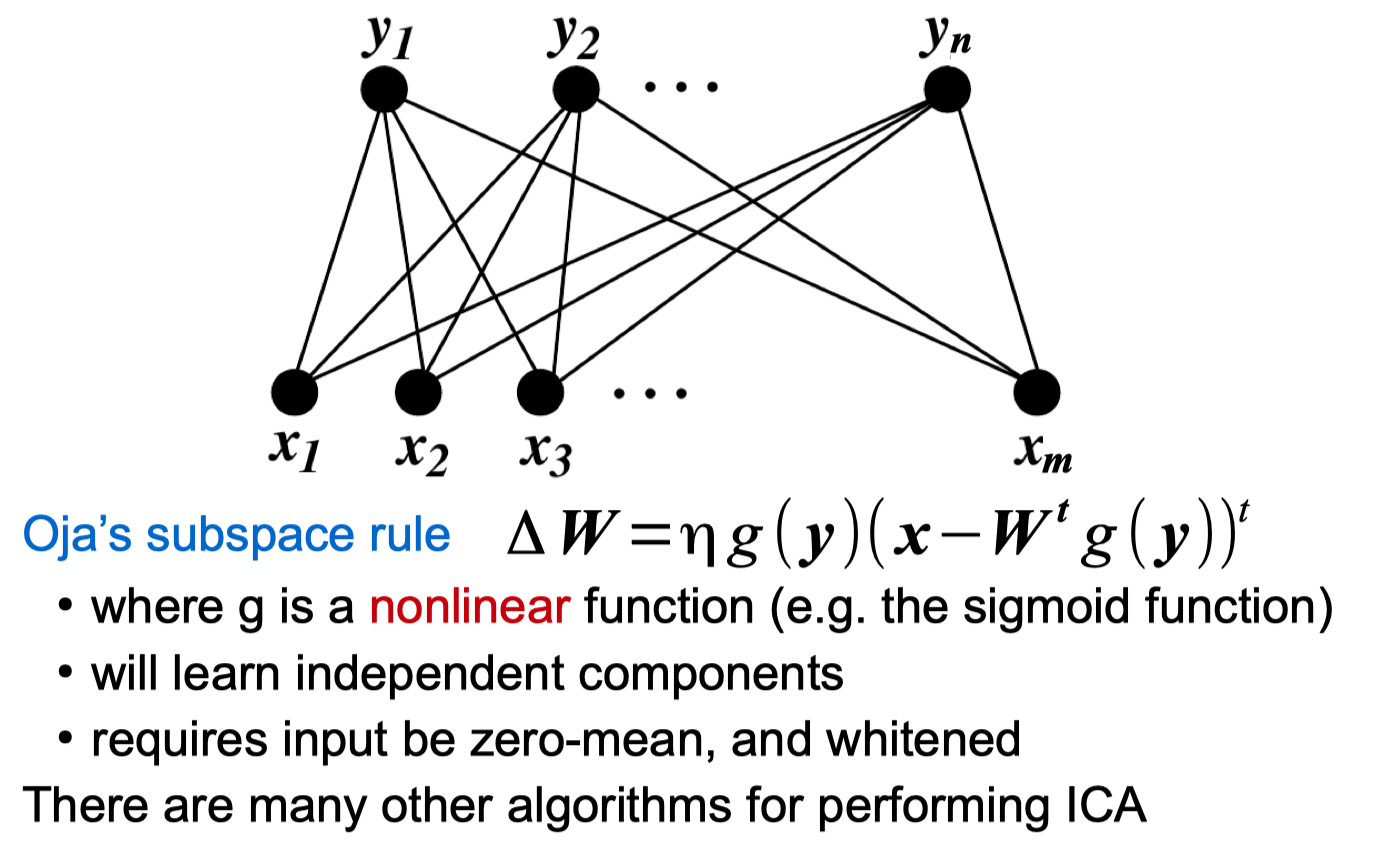
Random Projections


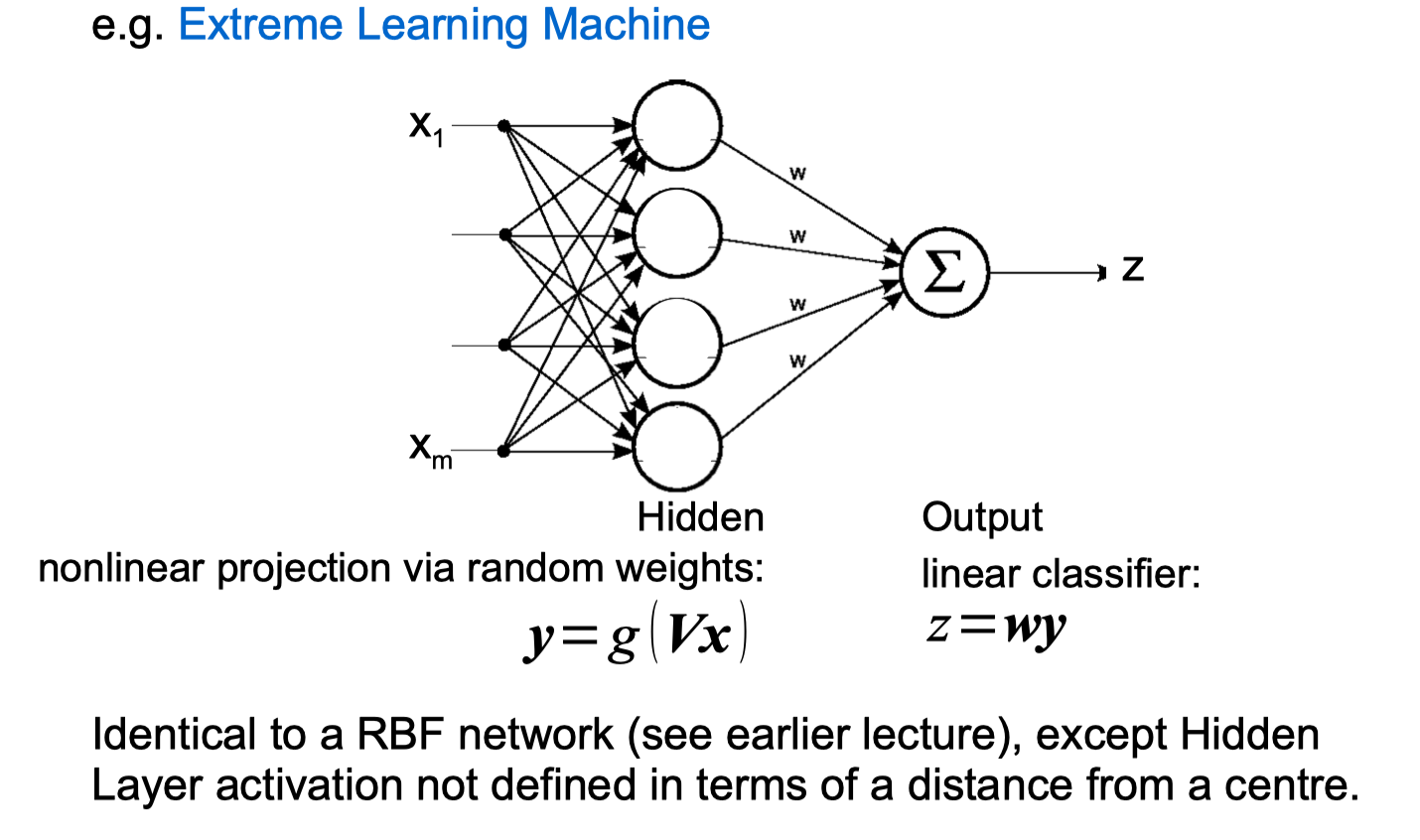



Sparse Coding


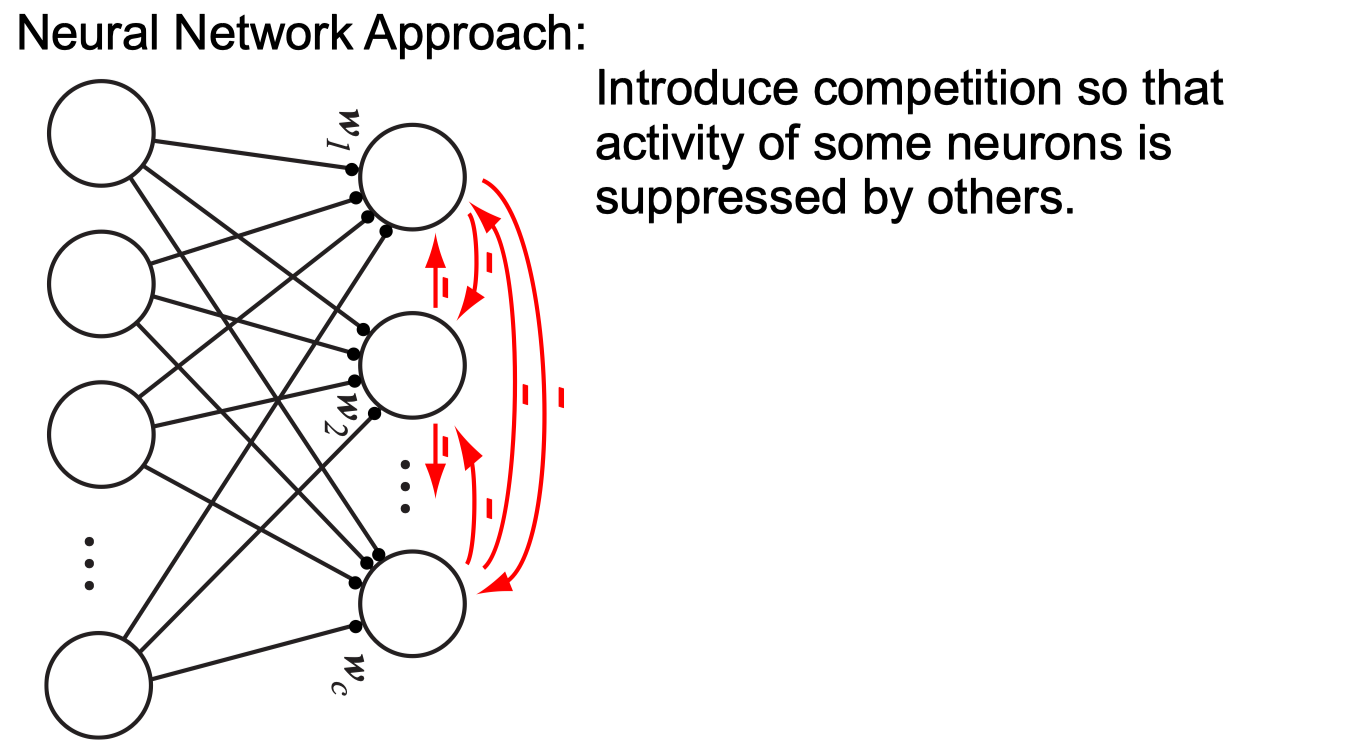
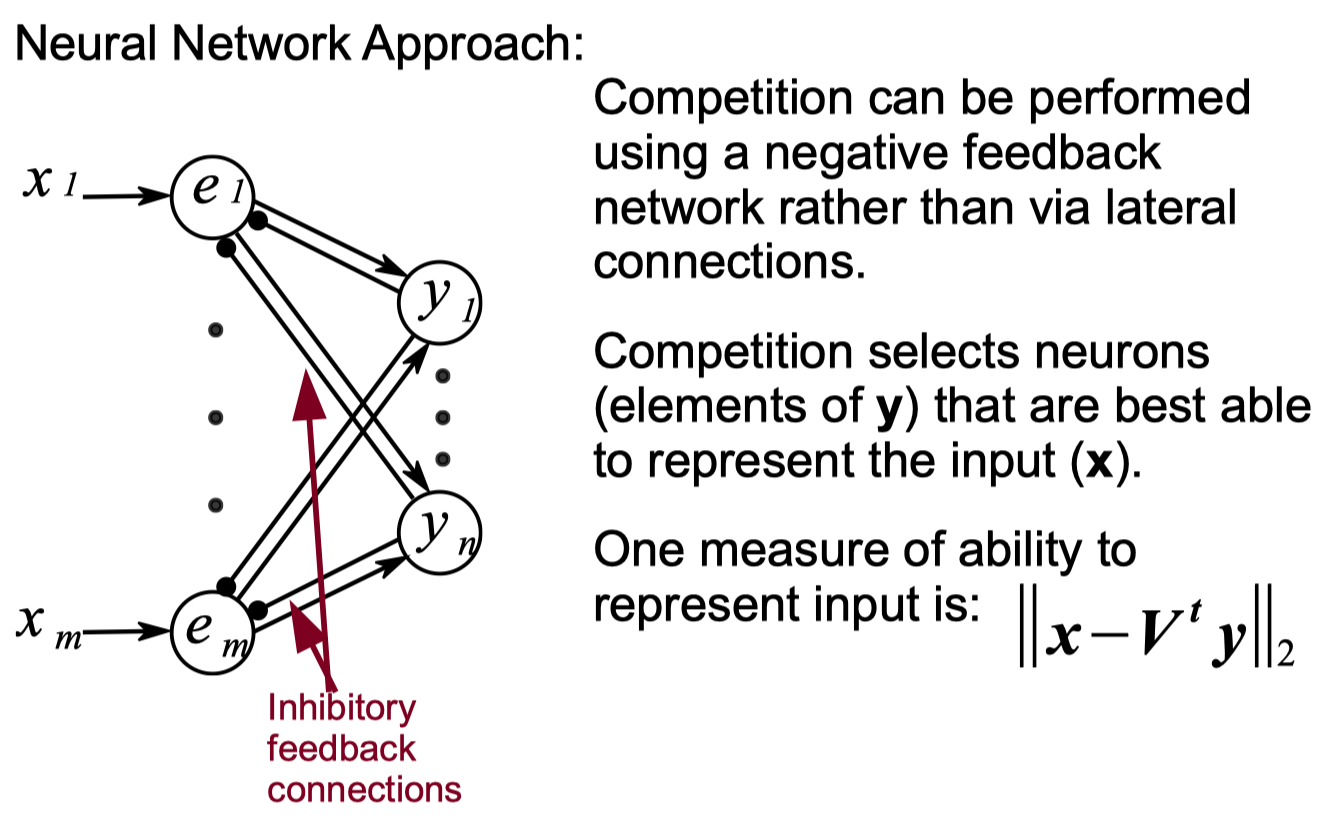
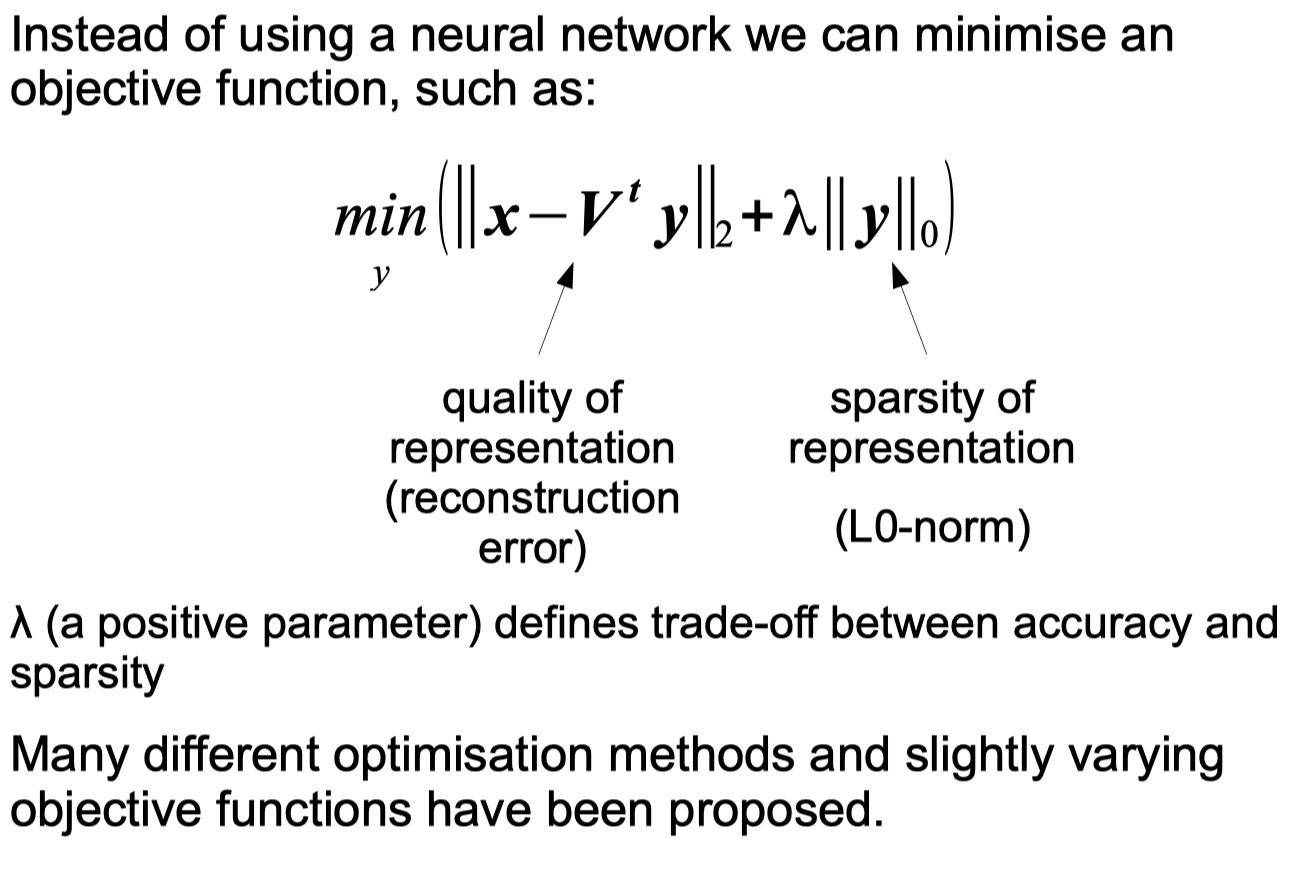

Sparse Coding python code
1
2
3
4
5
6
7
8
9
10
y2 = [0,0,1,0,0,0,-1,0]
V = [[0.4 ,0.55, 0.5, -0.1, -0.5, 0.9, 0.5, 0.45],[-0.6, -0.45, -0.5, 0.9, -0.5, 0.1, 0.5, 0.55]]
x = [-0.05,-0.95]
def error(x,V,y):
# x - Vy
temp = x - np.dot(V,np.transpose(y))
# educian
return np.sqrt(sum(np.power(temp,2)))
print(round(error(x,V,y2),4))
Output
1
0.0707
Comments powered by Disqus.