Support Vector Machines

Deep Learning: Support Vector Machines

Here is my Deep Learning Full Tutorial!

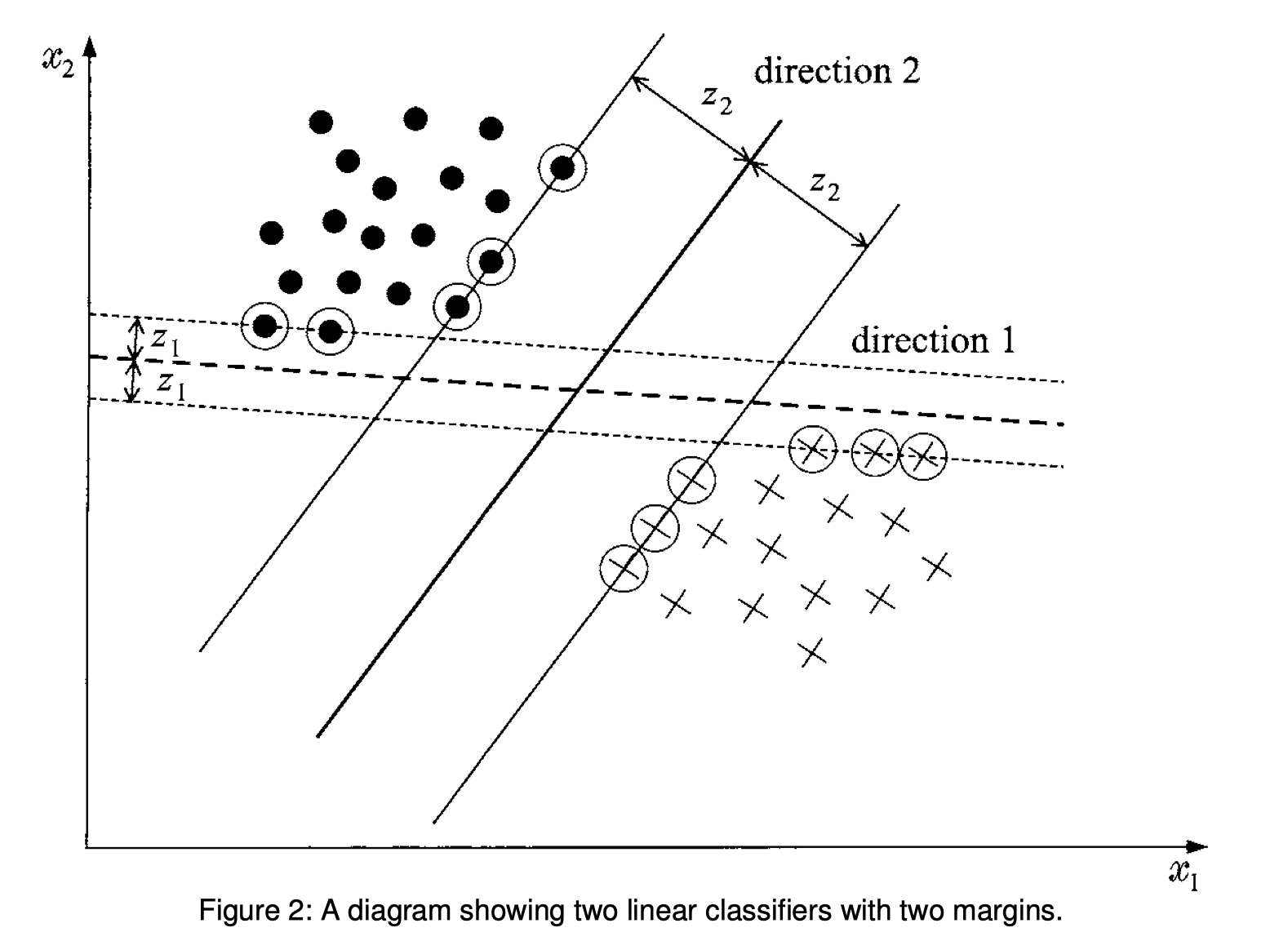
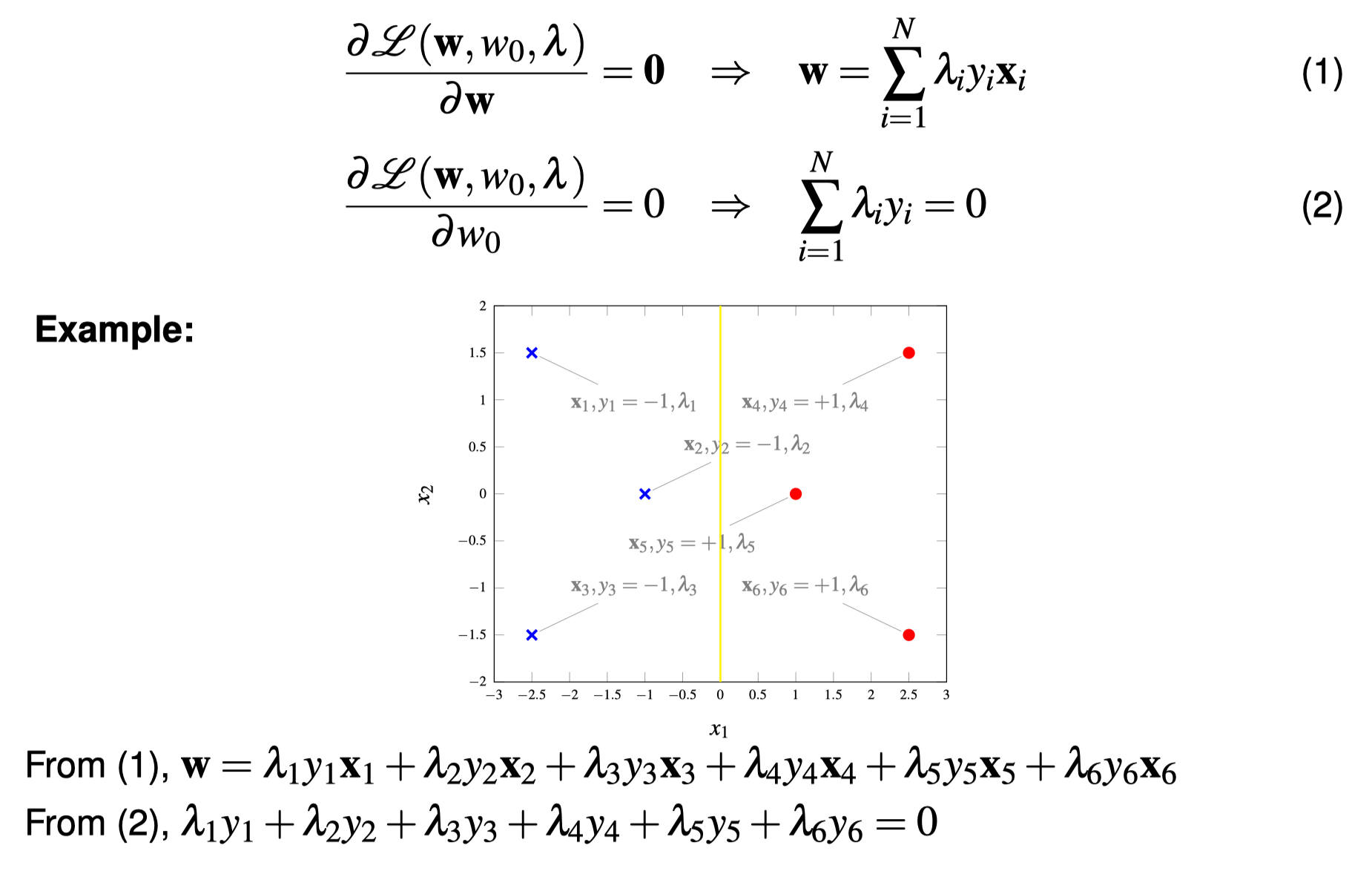
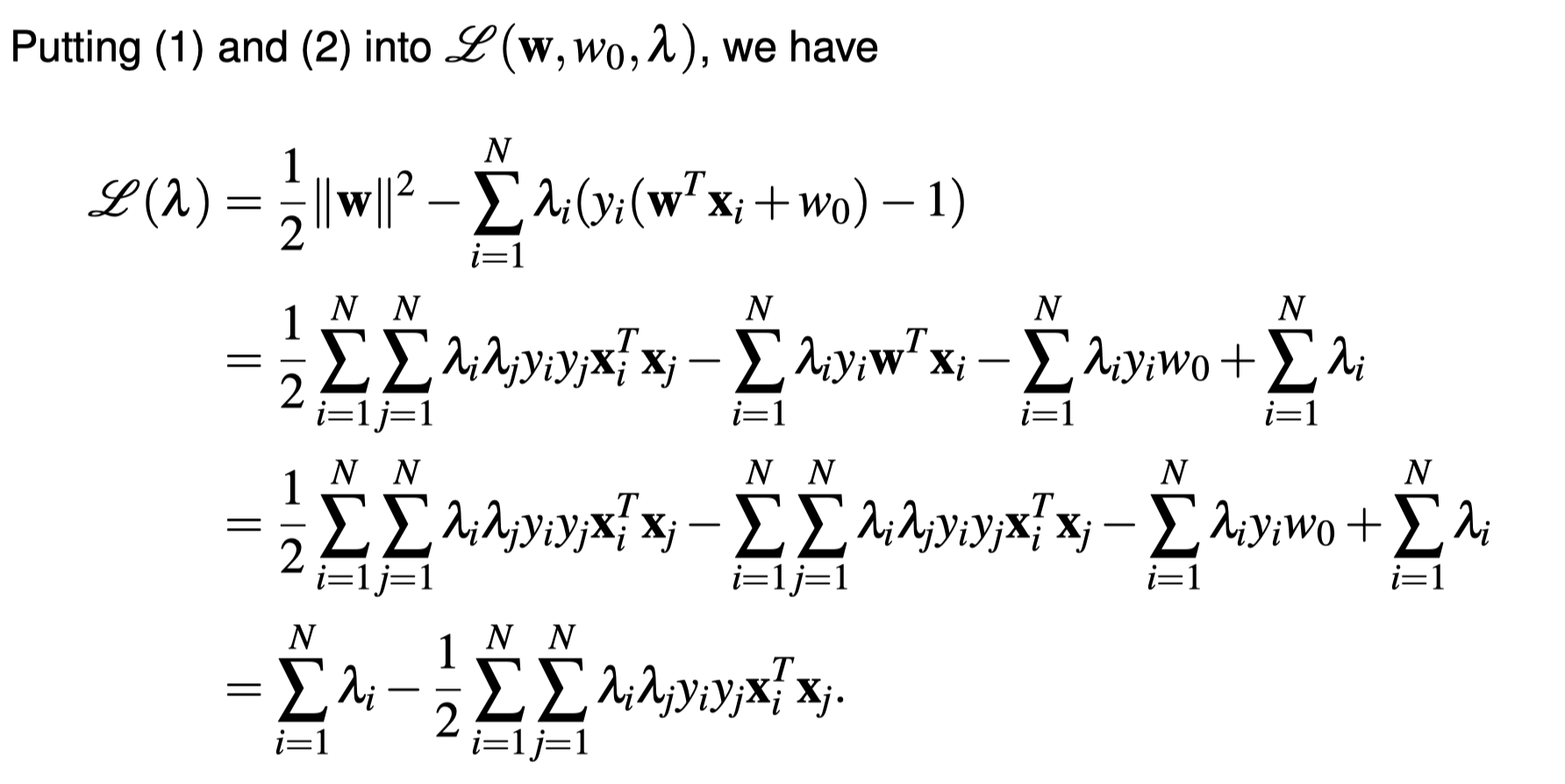
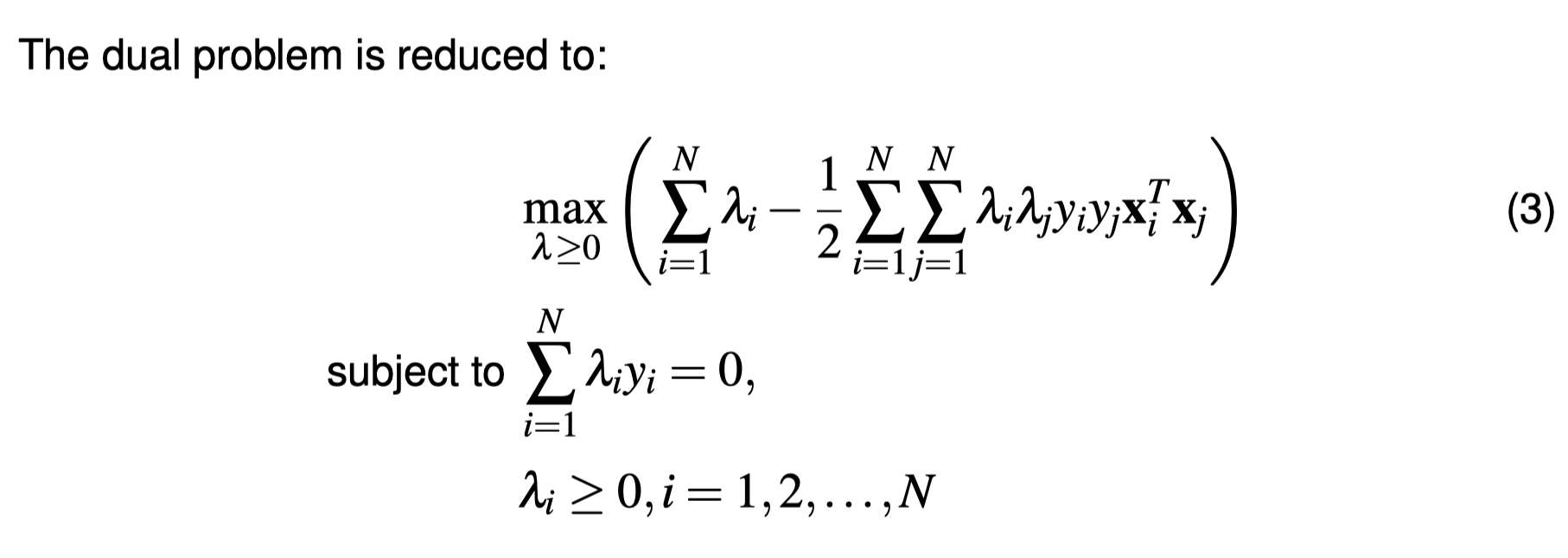
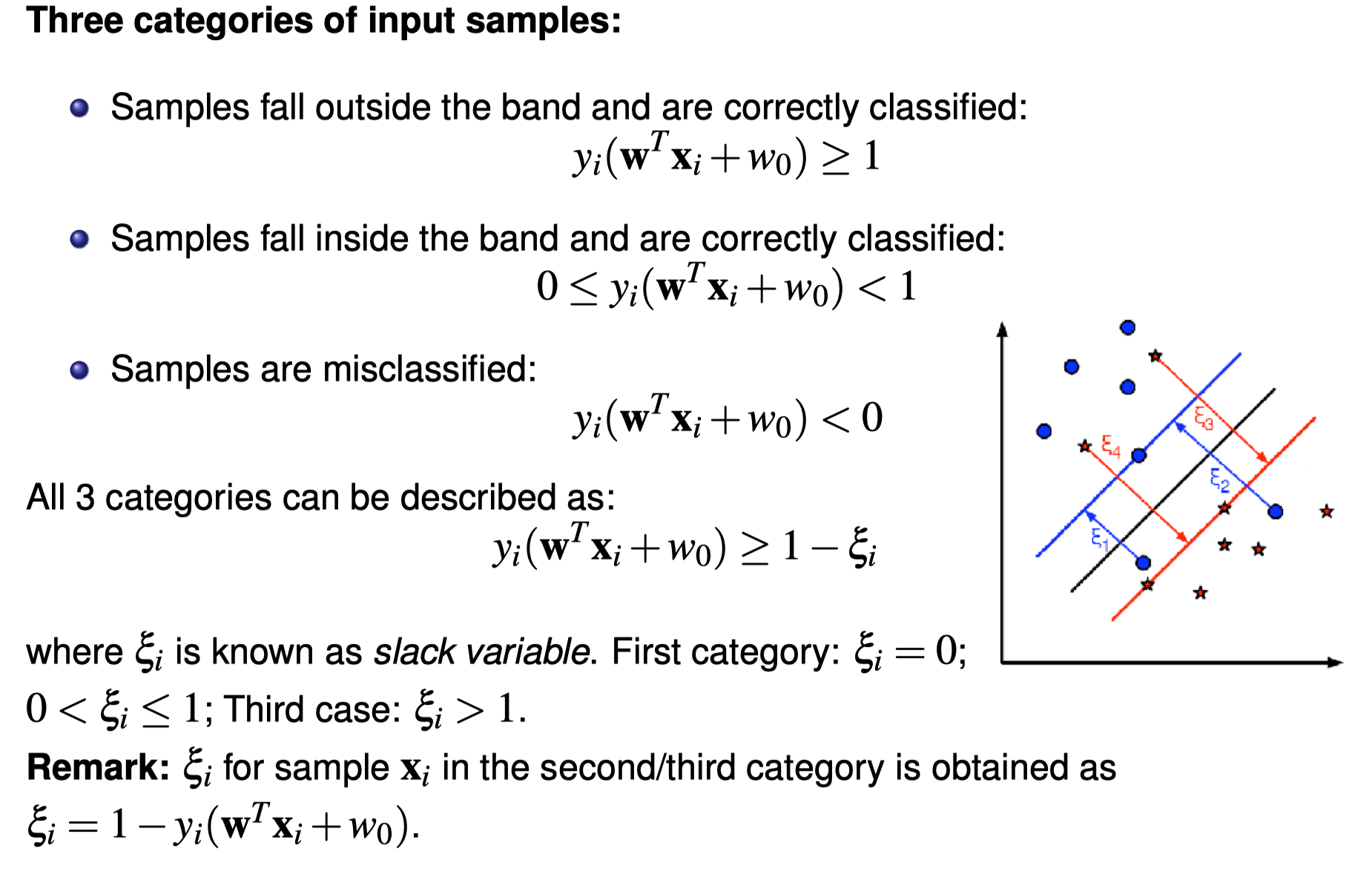
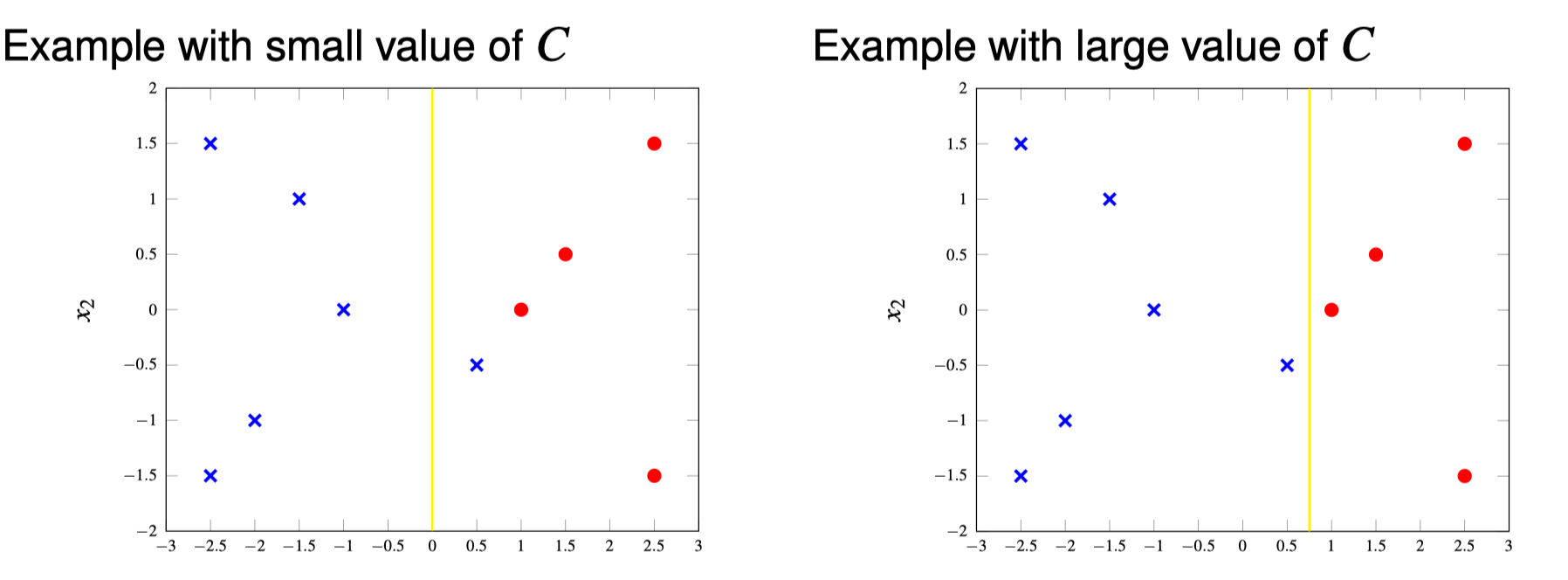
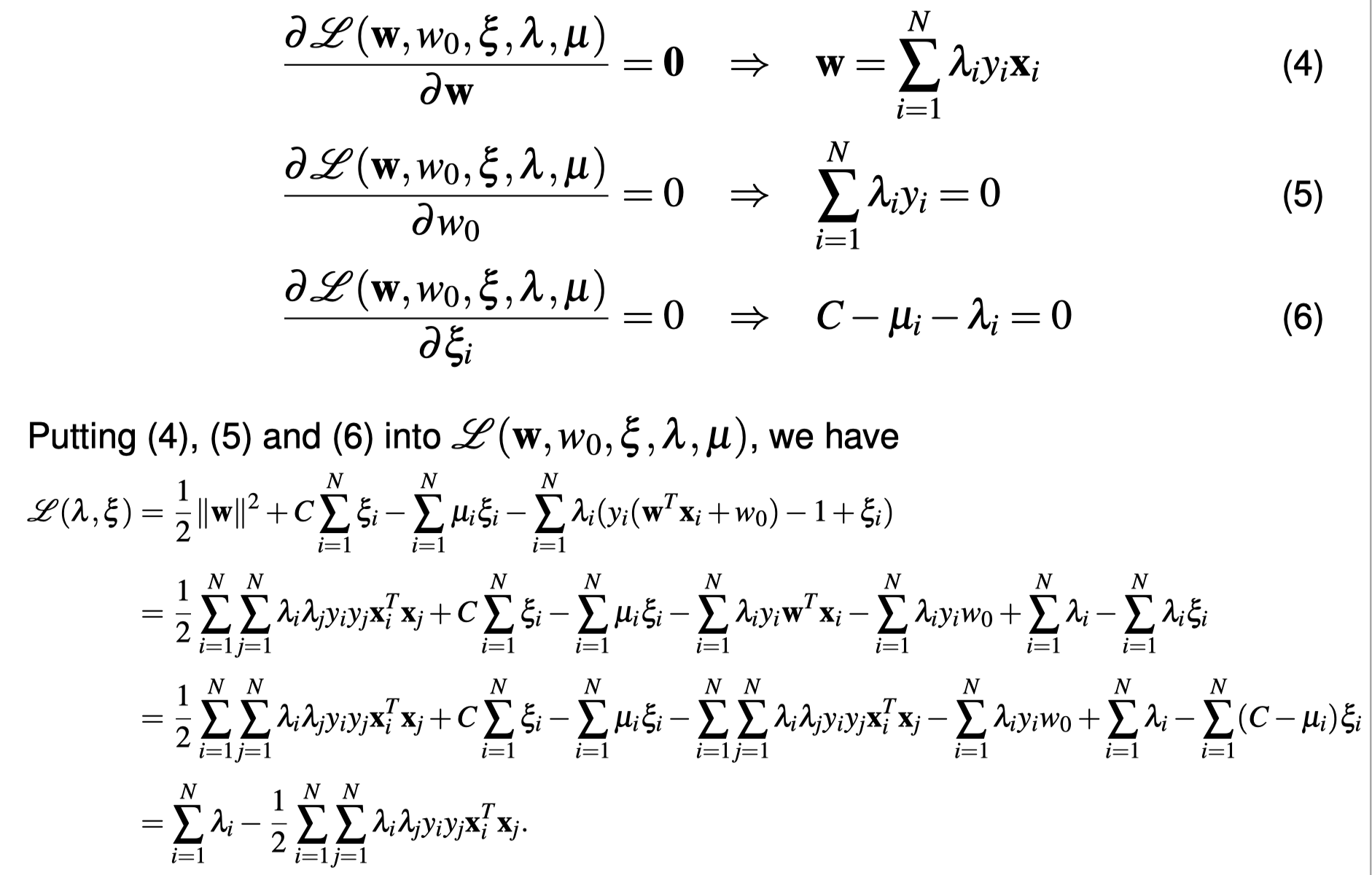
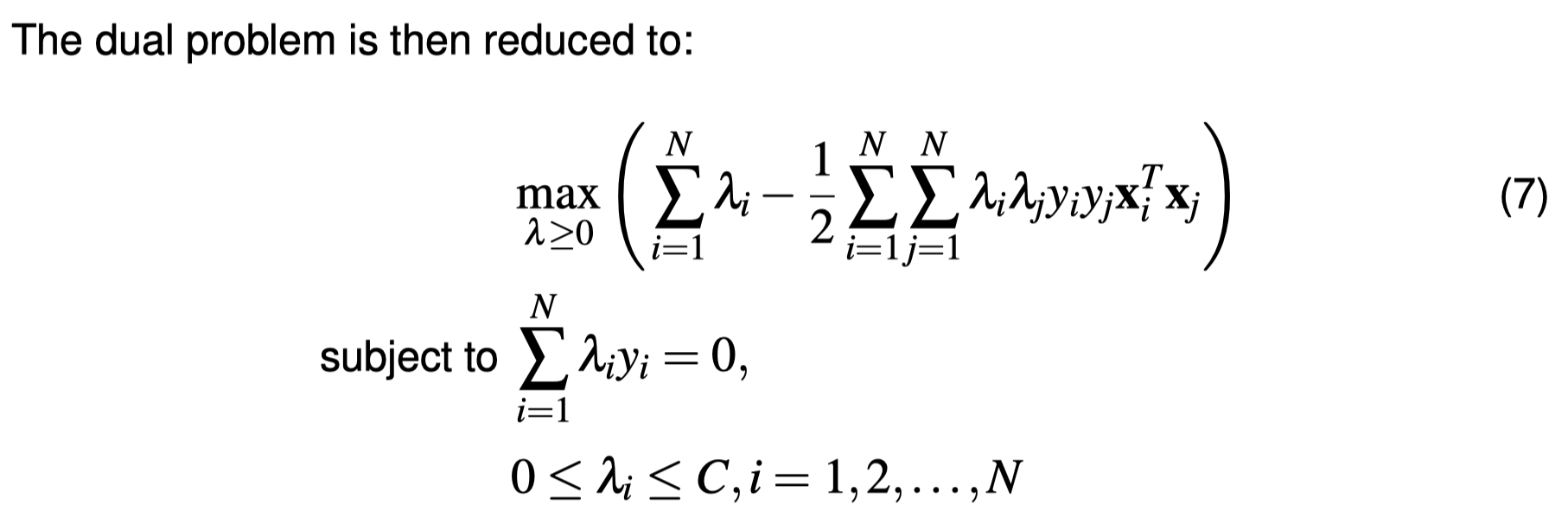
Nonlinear SVMs

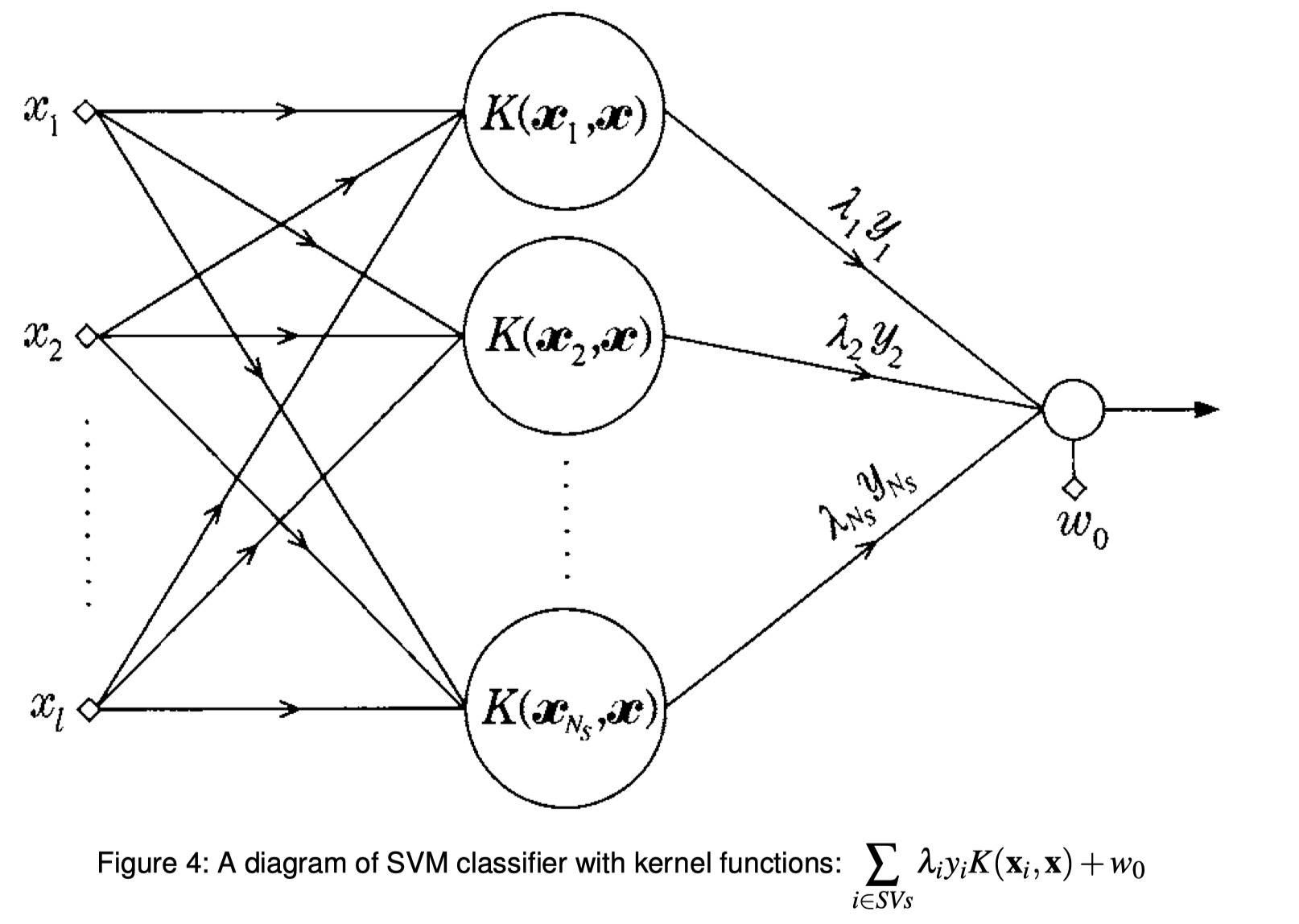
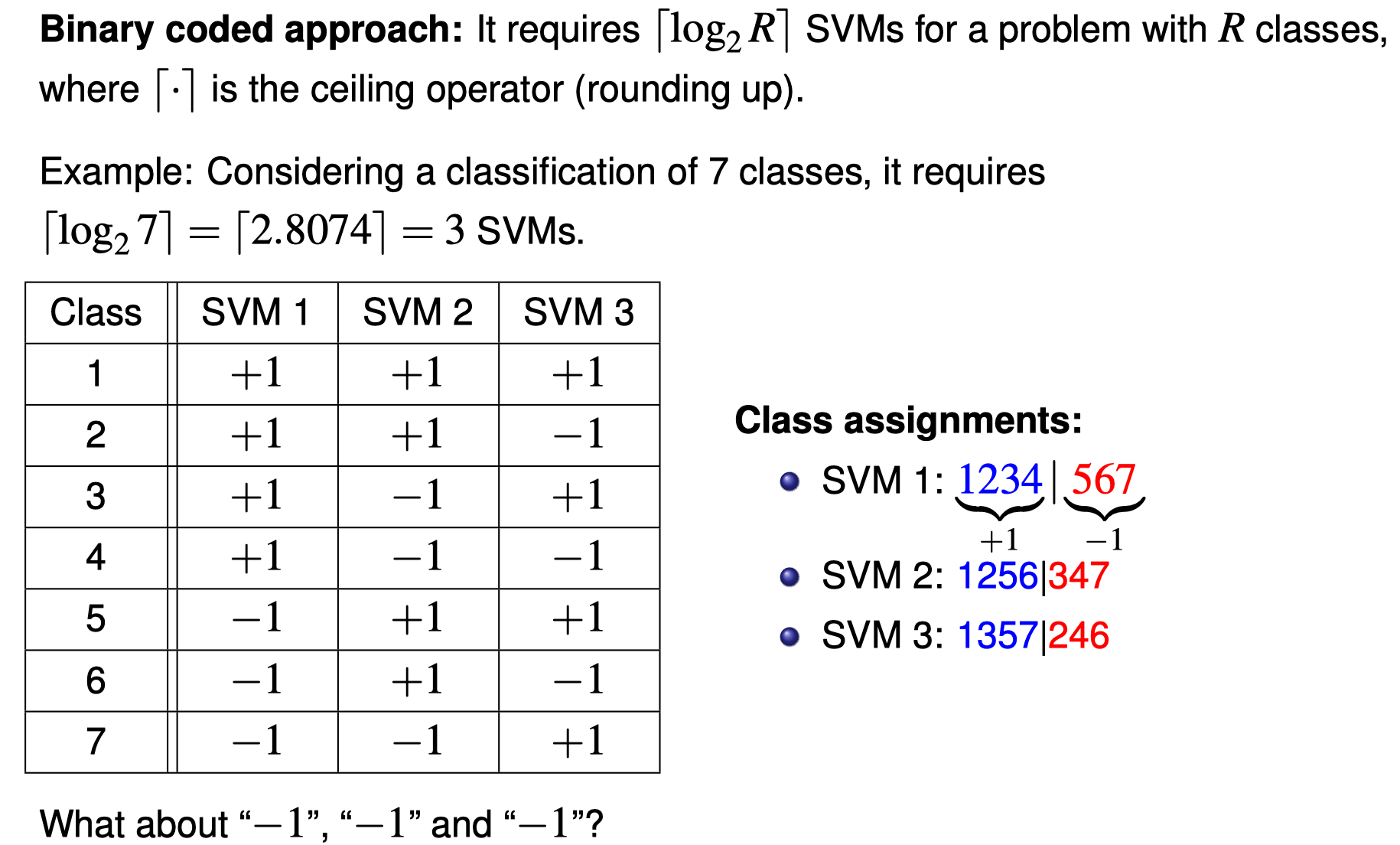
Multi-class SVMs

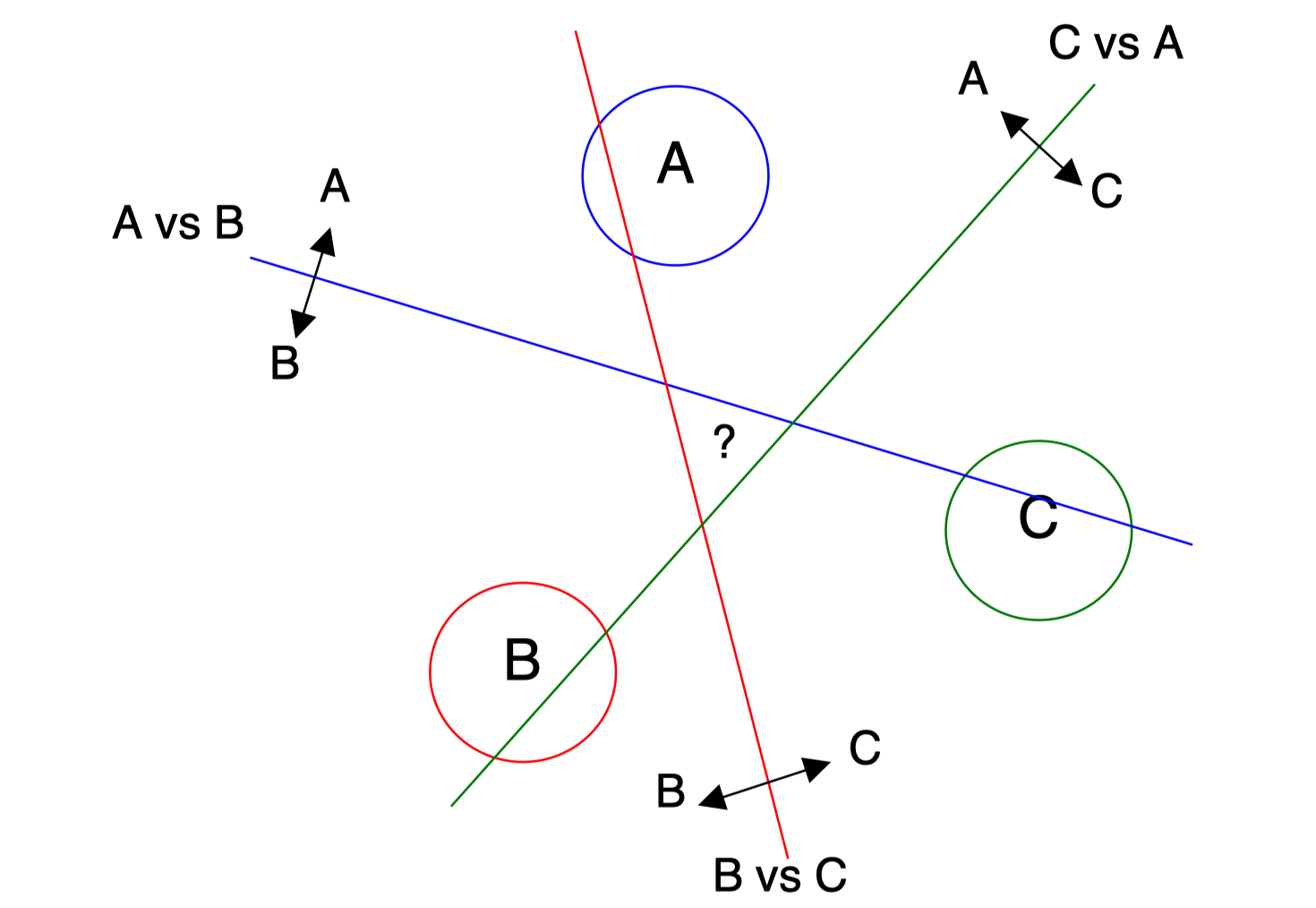
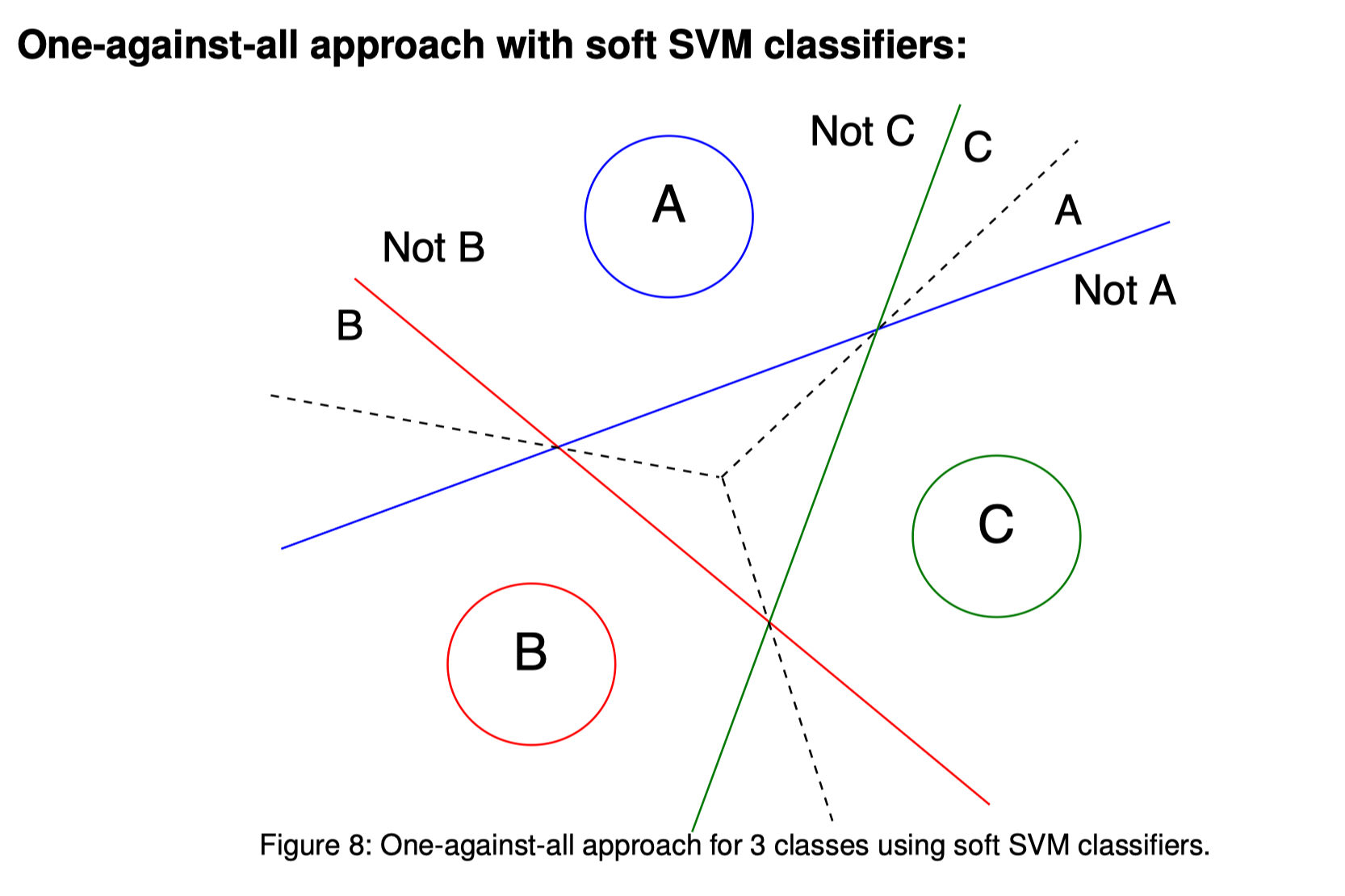
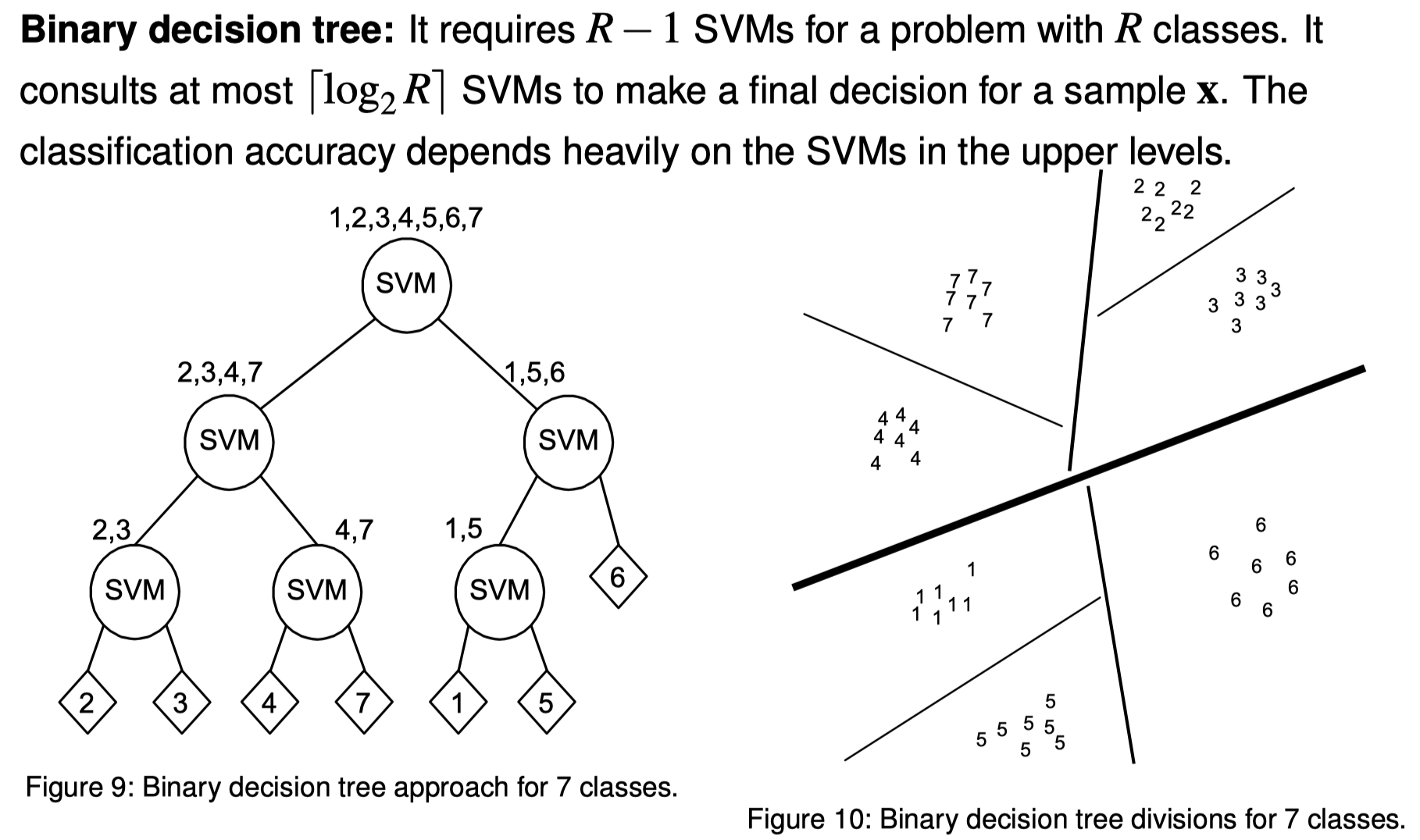
SVM find hyperplane by support vectors python code

def find_weight(support_vector_l, label_l):
    # First get the final result matrix from support vector labels
    # and sum of all lambda*lable(should equal to 0)
    lambdas_result_list = []
    for i in label_l:
        lambdas_result_list.append(i)
    lambdas_result_list.append(0)
    # Set a list to store data infront each lambda
    # e.g. 2(λ1) + 3(λ2) then we store 2 and 3 into the list
    # The data infront each lambda is the coordinate of support vectors
    lambdas = []
    lambdas_weight0 = []
    for i in range(len(label_l)):
        lambdas.append(label_l[i] * support_vector_l[i])
    lambdas = np.array(lambdas)
    # Store value infront lambda after calculate
    # yi((w^T)*x + w0) = 1
    for i in range(len(support_vector_l)):
        temp_list = []
        for data in lambdas:
            temp_list.append(np.dot(data, support_vector_l[i]))
        temp_list.append(1)
        lambdas_weight0.append(temp_list)

    # Store value infront lambdas from function:
    # sum all λiyi = 0
    # In this function only support vectors lambda is non-zero
    sum_of_lambdas = []
    for i in label_l:
        sum_of_lambdas.append(i)
    sum_of_lambdas.append(0)

    # Store the result from function mentioned above
    # prepare for matrix calculation
    lambdas_weight0.append(sum_of_lambdas)

    # Get the result of all unknown lambdas and weight0 from matrix operation
    # The calculation is like
    # [1, 2, 3, 4]    [λ1]   [1]
    # [5, 6, 7 ,8]  * [λ2] = [1]
    # [1, 3, 4, 6]    [λ3]   [-1]
    # [8, 6, 4, 2]    [λ4]   [0]
    # calculated by invert the left hand matrix and dot product it with the right hand matrix
    invers_matrix = np.linalg.inv(lambdas_weight0)
    lambda_weight0_result = np.dot(invers_matrix, lambdas_result_list)
    lambdas_result = lambda_weight0_result[:len(support_vector_l)]
    print(lambdas_result)
    weight0 = lambda_weight0_result[-1]
    # from all data we known get the w
    # where w = x1λ1 + x2λ2 +.......
    temp = []
    for index in range(len(lambdas)):
        temp.append(np.dot(lambdas[index], lambdas_result[index]))
    weight = np.sum(temp, axis=0, dtype=np.float32)
    return weight, weight0


support_v = np.array([[3,1], [3,-1], [1,0]])
label = [1, 1, -1]
w, w0 = find_weight(support_v, label)
print(w)
print(w0)

Output

[0.25 0.25 0.5 ]
[1. 0.]
-2.0